Je vous propose deux fonctions en VBA pour Access qui estiment la loi normale (ou loi de Laplace-Gauss) et son inverse en double précision. Pour rappel, Excel propose en standard ces fonctions (NORMDIST, NORMINV, NORMSDIST, NORMSINV) et des fonctions encore plus précises depuis Excel 2010 (NORM_DIST, NORM_INV, NORM_S_DIST, NORM_S_INV).
Loi normale
Cette fonction permet de trouver la probabilitĂ© cumulĂ©e (aire sous la courbe de la distribution gaussienne) d’une variable alĂ©atoire X.
Pour ce faire, je me suis appuyĂ© sur l’un des meilleurs algorithmes (dixit G. Marsaglia) pour calculer la fonction d’erreur complĂ©mentaire qui permet d’exprimer la fonction de rĂ©partition de la loi normale.
Cet algorithme est dĂ» Ă Takuya OOURA (1996) que j’ai implĂ©mentĂ© en VBA :
'Complementary error function in double precision
'http://www.kurims.kyoto-u.ac.jp/~ooura/index.html
'Copyright(C) 1996 Takuya OOURA : You may use, copy, modify this code for any purpose and without fee.
'Implementation en VBA par Philben - v1.0
Const C0 As Double = 1.27109764952614E-03 + 9.2E-19, C1 As Double = 1.1931402283834E-04 + 9.44E-19, _
C2 As Double = 3.96385097360513E-03 + 5E-18, C3 As Double = 8.70779635317295E-04 + 8.28E-19, _
C4 As Double = 7.73672528313526E-03 + 6.68E-18, C5 As Double = 3.83335126264887E-03 + 3.03E-18, _
C6 As Double = 1.27223813782122E-02 + 7.55E-17, C7 As Double = 0.013382364453346 + 6.9E-18, _
C8 As Double = 1.61315329733252E-02 + 2.48E-17, C9 As Double = 3.90976845588484E-02 + 3.5E-18, _
C10 As Double = 2.49367200053503E-03 + 3.04E-18
Const C11 As Double = 8.38864557023001E-02 + 9.92E-17, C12 As Double = 0.119463959964325 + 4.15E-16, _
C13 As Double = 1.66207924969367E-02 + 3.56E-17, C14 As Double = 0.357524274449531 + 4.3E-17, _
C15 As Double = 0.80527640875291 + 5.67E-16, C16 As Double = 1.18902982909273 + 3.33E-15, _
C17 As Double = 1.37040217682338 + 1.67E-15, C18 As Double = 1.31314653831023 + 9.8E-16, _
C19 As Double = 1.07925515155856 + 6.77E-15, C20 As Double = 0.774368199119538 + 6.09E-16, _
C21 As Double = 0.490165080585318 + 4.24E-16, C22 As Double = 0.275374741597376 + 7.82E-16
Dim t As Double, u As Double, y As Double
t = 3.97886080735226 / (Abs(X) + 3.97886080735226)
u = t - 0.5
y = (((((((((C0 * u + C1) * u - C2) * u - C3) * u + C4) * u + C5) * u - C6) * u - C7) * u + C8) * u + C9) * u + C10
y = ((((((((((((y * u - C11) * u - C12) * u + C13) * u + C14) * u + C15) * u + C16) * u + C17) * u + C18) * u + C19) * _
u + C20) * u + C21) * u + C22) * t * Exp(-X * X)
If X < 0 Then derfc = 2 - y Else: derfc = y
End Function
La prĂ©cision de la version VBA est certainement moins bonne que la version en C de Takura Ooura car il utilise des constantes avec plus de 15 chiffres significatifs. En effet, VBA n’affiche que 15 chiffres pour le type Double bien qu’il conserve en faite 16 chiffres en interne…
Pour cette raison, chaque constante est définie comme la somme de deux nombres pour conserver ce 16ème chiffre de précision.
La fonction VBA pour calculer la loi normale est :
' Procédure : LoiNormale [Function]
' Auteur : Philben - Free to use
' Retour : Double
' Version : 2.0
' Objet : Détermine la probabilité cumulée ou non d'une distribution normale en fonction
' : d'une variable X, de la moyenne et de l'Ă©cart-type de la distribution
' Historique : v2.0 : Double précision (07/2012)
' v1.0 : Simple précision (07/2007)
'---------------------------------------------------------------------------------------
Public Function LoiNormale(ByVal X As Double, _
Optional ByVal Esperance As Double = 0, _
Optional ByVal EcartType As Double = 1, _
Optional CumulProbabilite As Boolean = True) As Double
If EcartType <= 0 Then
LoiNormale = -1
Else
If CumulProbabilite Then
LoiNormale = derfc((Esperance - X) / (EcartType * Sqr(2))) * 0.5
Else
X = (X - Esperance) / EcartType
LoiNormale = Exp(-X * X * 0.5) / (EcartType * Sqr(8 * Atn(1)))
End If
End If
End Function
Les paramètres sont la variable alĂ©atoire X pour laquelle on cherche la probabilitĂ© correspondante, l’espĂ©rance de la distribution (moyenne mu), l’Ă©cart-type de la distribution (standard deviation in english) et ‘CumulProbabilite’ un boolĂ©en Ă vrai (par dĂ©faut) si on souhaite obtenir la probabilitĂ© cumulĂ©e de la fonction de rĂ©partition.
Par dĂ©faut, l’espĂ©rance est 0 et l’Ă©cart-type Ă 1 ce qui correspond aux paramètres la loi normale centrĂ©e rĂ©duite (ou standard) N(0,1) d’espĂ©rance Ă©gale Ă 0 et de variance Ă©gale Ă 1.
Loi normale inverse
Cette fonction permet de trouver la variable alĂ©atoire X associĂ©e Ă une probabilitĂ© cumulĂ©e. Ooura propose aussi un algorithme qui calcul l’inverse de la fonction d’erreur complĂ©mentaire qui permet d’obtenir des rĂ©sultats meilleurs qu’une recherche par bisection avec la fonction derfc.
'Inverse of complementary error function in double precision
'http://www.kurims.kyoto-u.ac.jp/~ooura/index.html
'Copyright(C) 1996 Takuya OOURA : You may use, copy, modify this code for any purpose and without fee.
'Implementation en VBA par Philben - v1.0
Const C0 As Double = 1.12648096188977E-03 + 9.22E-18, C1 As Double = 1.05739299623423E-04 + 4.7E-20, _
C2 As Double = 0.003512871461291 + 2.5E-19, C3 As Double = 7.7170835895412E-04 + 9.39E-19, _
C4 As Double = 6.85649426074558E-03 + 6.12E-18, C5 As Double = 3.39721910367775E-03 + 8.61E-18, _
C6 As Double = 1.12749169332504E-02 + 8.7E-17, C7 As Double = 1.18598117047771E-02 + 1.04E-17, _
C8 As Double = 1.42961988697898E-02 + 1.8E-18, C9 As Double = 3.46494207789099E-02 + 9.22E-17, _
C10 As Double = 2.20995927012179E-03 + 6.7E-19
Const C11 As Double = 7.43424357241784E-02 + 8.61E-17, C12 As Double = 0.105872177941595 + 4.88E-16, _
C13 As Double = 1.47297938331485E-02 + 1.21E-17, C14 As Double = 0.316847638520135 + 9.44E-16, _
C15 As Double = 0.71365763586873 + 3.64E-16, C16 As Double = 1.05375024970847 + 1.38E-15, _
C17 As Double = 1.21448730779995 + 2.37E-15, C18 As Double = 1.1637458193156 + 8.31E-15, _
C19 As Double = 0.956464974744799 + 6E-18, C20 As Double = 0.686265948274097 + 8.16E-16, _
C21 As Double = 0.43439749233143 + 1.15E-16, C22 As Double = 0.24404451059319 + 9.35E-16, _
C23 As Double = 0.120782237635245 + 2.22E-16
Dim s As Double, t As Double, u As Double, w As Double, X As Double, z As Double
If y > 1 Then z = 2 - y Else: z = y
w = 0.916461398268964 - Log(z)
u = Sqr(w)
s = (Log(u) + 0.488826640273108) / w
t = 1 / (u + 0.231729200323405)
X = u * (1 - s * (s * 0.124610454613712 + 0.5)) - ((((-7.28846765585675E-02 * t + 0.269999308670029) * _
t + 0.150689047360223) * t + 0.116065025341614) * t + 0.499999303439796) * t
t = 3.97886080735226 / (X + 3.97886080735226)
u = t - 0.5
s = (((((((((C0 * u + C1) * u - C2) * u - C3) * u + C4) * u + C5) * u - C6) * u - C7) * u + C8) * u + C9) * u + C10
s = ((((((((((((s * u - C11) * u - C12) * u + C13) * u + C14) * u + C15) * u + C16) * u + C17) * u + _
C18) * u + C19) * u + C20) * u + C21) * u + C22) * t - z * Exp(X * X - C23)
X = X + (s * (X * s + 1))
If y > 1 Then dierfc = -X Else: dierfc = X
End Function
La fonction VBA pour calculer l’inverse de la loi normale :
' Procédure : LoiNormaleInverse [Function]
' Auteur : Philben - Free to use
' Retour : Double
' Version : 2.0
' Objet : DĂ©termine la variable X d'une distribution normale en fonction de
' : sa probabilité cumulée Pc, de la moyenne et de l'écart-type de la distribution
' Historique : v2.0 : Double précision (07/2012)
' v1.0 : Simple précision (07/2007)
'---------------------------------------------------------------------------------------
Public Function LoiNormaleInverse(ByVal Pc As Double, _
Optional ByVal Esperance As Double = 0, _
Optional ByVal EcartType As Double = 1) As Double
If Pc <= 0 Then
LoiNormaleInverse = -99
ElseIf Pc >= 1 Then
LoiNormaleInverse = 99
Else
LoiNormaleInverse = (-dierfc(Pc * 2) * EcartType * Sqr(2)) + Esperance
End If
End Function
Les paramètres sont la probabilitĂ© cumulĂ©e, l’espĂ©rance et l’Ă©cart-type de la distribution gaussienne pour lesquels on recherche X.
Précision des résultats
Par comparaison avec les résultats de la fonction Excel NORM_S_DIST (notre référence Excel 2010) sur la plage de valeurs entre -8 et 8 de la loi normale standard avec un incrément de 1E-05, la plus grande différence relevée est de 2,220E-16 et une erreur relative maximum de 1,490E-14.
Exemples
Coller l’ensemble des fonctions dans un module standard VBA. Dans la fenĂŞtre d’exĂ©cution de l’Ă©diteur visual basic (CTRL + G pour la faire apparaĂ®tre) coller la ou les lignes d’exemples qui commence par ?, mettre le focus sur la ligne Ă exĂ©cuter puis appuyer sur la touche ‘EntrĂ©e’ pour voir le rĂ©sultat.
Quelle est la probabilitĂ© pour qu’une variable alĂ©atoire X soit infĂ©rieure ou Ă©gale Ă 14 si elle suit la loi normale N(10,16) (espĂ©rance = 10 et variance = 16) ?
L’aire sous la courbe de couleur bleue est la probabilitĂ© attendue :
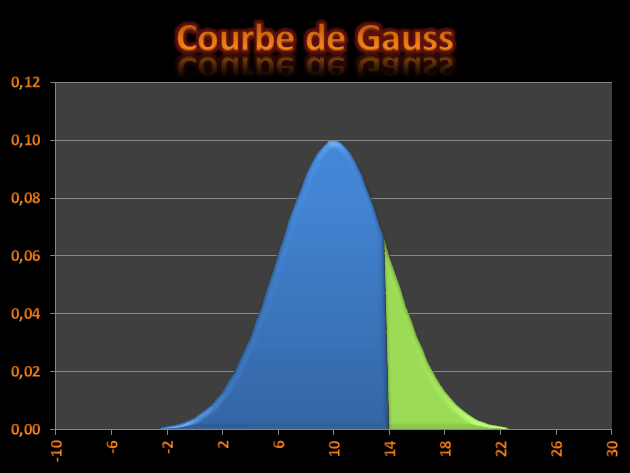
Sachant que l’Ă©cart-type est la racine carrĂ©e de la variance :
?LoiNormale(14,10,SQR(16))
Remarque : La loi normale est une loi continue de – l’infini Ă + l’infini et la probabilitĂ© que X soit Ă©gal Ă une valeur est pratiquement nulle (P(X = 14) = 0). Donc P(X <= 14) = P(X < 14). InversĂ©ment, comment retrouver la variable X de cette probabilitĂ© ?
?LoiNormaleinverse(0.841344746068543,10,sqr(16))
Quelle est la probabilité complémentaire de X : P(X > 14) (Aire verte de la courbe) ?
La loi normale est une loi symétrique, on peut donc écrire :
?1-LoiNormale(14,10,sqr(16))
ou encore :
?LoiNormale(10-(14-10),10,SQR(16))
Cette deuxième Ă©criture est plus simple dans le cas d’une loi normale centrĂ©e rĂ©duite N(0,1) :
Exemple pour la probabilité complémentaire de X = 2 (P = 0.977249868051821 et 1-P = 2.27501319481792E-02)
?LoiNormale(-2)
Remarque : Sous certaines conditions, la loi normale permet d’approximer les lois de Poisson et Binomiale.
Quelle est la probabilité que 7 <= X <= 9 sachant que X suit une loi normale N(8;2,25) (espérance = 8 et variance = 2,25) ?
La probabilitĂ© recherchĂ©e est l’aire de la courbe verte :
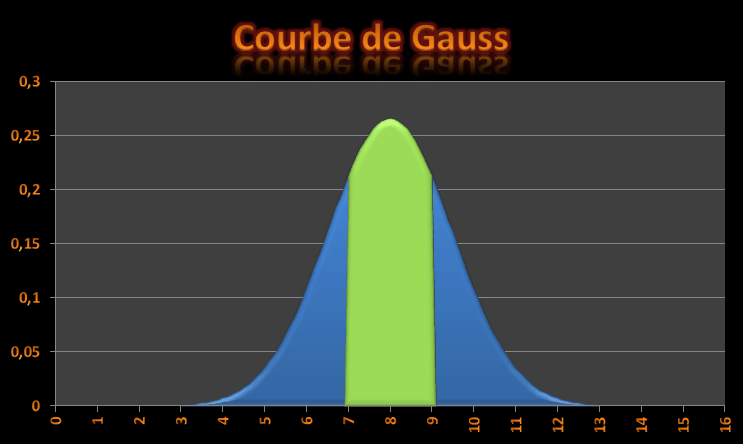
Dans cet exemple, les Ă©carts Ă l’espĂ©rance sont symĂ©trique (7 + 1 = 8 et 9 – 1 = 8) on peut Ă©crire :
?2*loinormale(9,8,sqr(2.25))-1
'Probabilité attendue : 0.495014924906154
?1-2*loinormale(7,8,sqr(2.25))
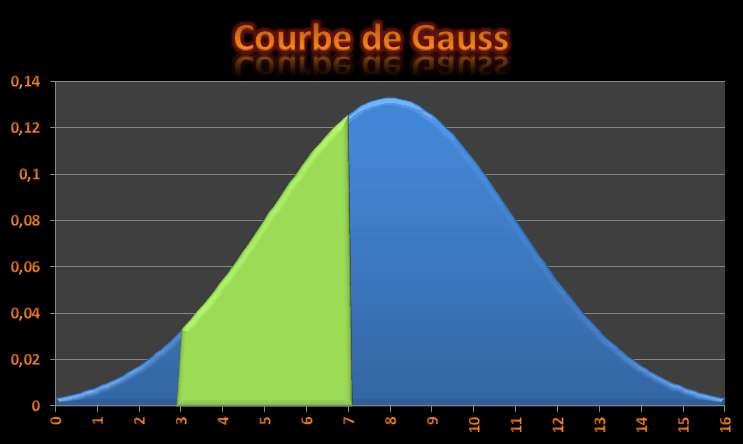
Dans le cas général, il faut soustraire les deux probabilités. Par exemple pour 3 <= X <= 7 sachant que X suit une loi normale N(8;9), la formule devient :
?loinormale(7,8,3)-loinormale(3,8,3)
Exactitude des résultats
L’objectif est d’Ă©tudier succinctement l’exactitude des rĂ©sultats fournis par les fonctions Excel et les fonctions dĂ©crites ci-dessus.
Pour ce faire je me suis servi comme référence des probabilités cumulées fournies par Maple 7 de la loi normale standard (avec plus de 16 chiffres significatifs) pour Z<=-1, Z<=-2, Z<=-3, ..., Z<=-37
Le 1er graphe affiche l'erreur relative commise sur l'approximation des probabilités en fonction de Z.
L'ordonnée est exprimée en log10 des erreurs relatives. Par exemple, le calcul de l'ordonnée avec la fonction Excel 2010 pour Z = -1 est :
-Log(Abs(WorksheetFunction.Norm_S_Dist(-1, True) - (0.158655253931457 + 5.141E-17))/ (0.158655253931457 + 5.141E-17)) / Log(10)
En pratique, il faut vĂ©rifier que la diffĂ©rence soit supĂ©rieure Ă zĂ©ro car Log(0) provoque une erreur…
ThĂ©oriquement, la valeur maximale est 16 lorsqu’il n’existe aucune diffĂ©rence entre les deux valeurs car le type Double a une prĂ©cision de 16 chiffres (15 visibles + 1) : -Log(1E-16 / 1) / Log(10). Si on ne considère que les 15 chiffres visibles, l’exactitude est dĂ©jĂ parfaite pour une valeur de 15.
En rĂ©sumĂ©, plus la valeur du log de l’erreur relative est Ă©levĂ©e plus le rĂ©sultat est exact.
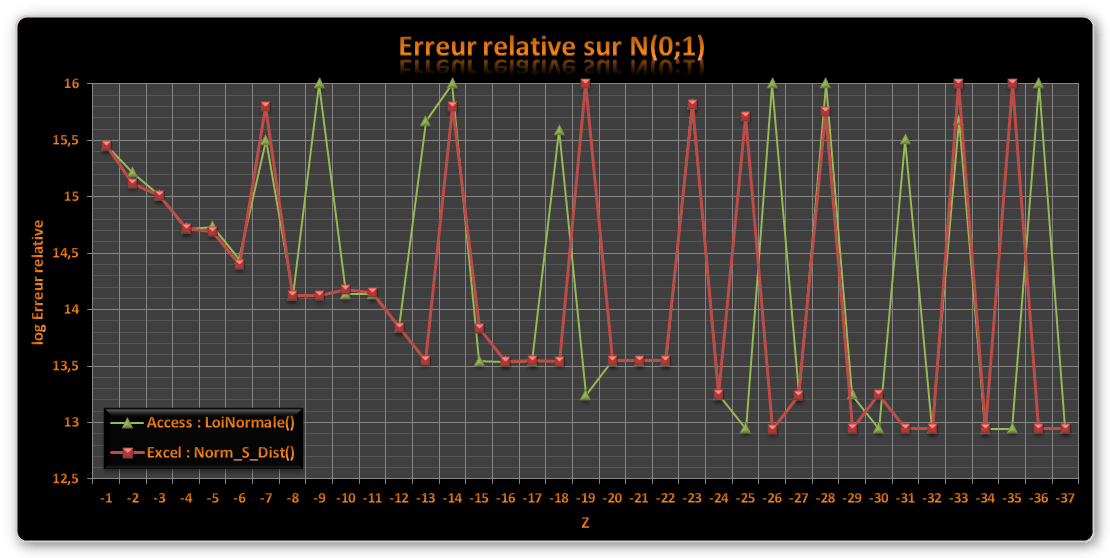
Les résultats entre Excel et Access sont très proches.
Le 2ème graphe affiche l’erreur relative commise sur l’approximation de z en fonction des probabilitĂ©s pour comparer les fonctions Norm_S_Inv() d’Excel 2010 et LoiNormaleInverse().
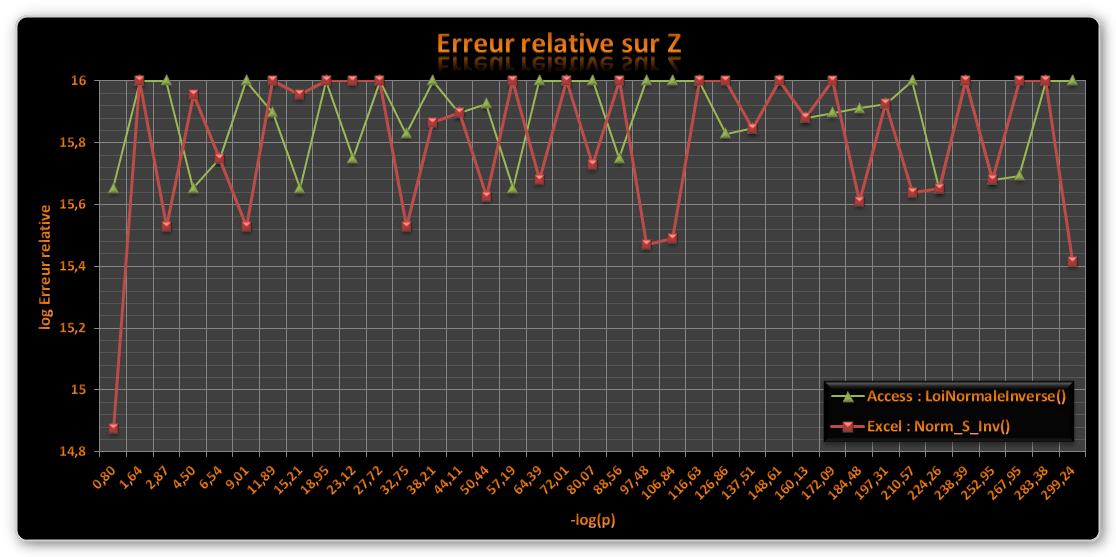
Les rĂ©sultats entre Excel et Access sont très proches, on peut noter une petite faiblesse d’Excel sur l’approximation de z pour la 1ère probabilitĂ© (z=-1 thĂ©oriquement).
@+
Philippe


Merci encore pour ce prĂ©cieux code qui m’a bien aidĂ© aujourd’hui