Après avoir vu différents algorithmes de similarité dans des billets précédents, je vous propose un petit comparatif à travers un exemple qui consiste à trouver le doublon de restaurants par leur nom, adresse, téléphone et type de cusine.

Les données
Les données sont issues d’un exemple connu de recherche de doublons et sont présentées ici dans une seule colonne où nom, adresse, téléphone et type de cuisine sont fusionnés. Le fichier de données contient 224 lignes et chaque resto possède un et un seul doublon. Cet exemple reste donc plus simple qu’un cas général de recherche de doublons…
Extrait du fichier :

Une difficulté s’ajoute pour le dernier restaurant car les ‘é’ de Célébrités sont convertis en HTML (& eacute;)…

Le fichier source original est ici.

Principe
Le principe est donc de rechercher pour chaque ligne, le restaurant qui a la similarité la plus forte soit 49 952 mesures (224 x 223) après conversion des chaînes en majuscule.
Pour chaque restaurant, je considère que le bon doublon a été correctement trouvé s’il arrive avec le plus fort indice par rapport aux 222 autres restaurants.
J’ai comparé les 3 algorithmes Jaro-Winkler (JW), Damerau-Levenshtein (DL) et les 6 indices Cosinus/Dice/Jaccard/… (IS), en recherchant pour chacun la meilleure configuration.

Résultats
Concernant DL, pas de problème pour trouver la meilleure configuration car il suffit de passer les 2 chaînes en argument de la fonction.
Damerau-Levenshtein a permis de détecter 185 doublons sur 224 soit 82,6% de réussite.

Concernant Jaro-Winkler, on peut jouer sur la longueur du préfixe entre 0 et 4. Les résultats obtenus sont :

Dans cet exemple, la meilleure longueur de préfixe est 2 avec 214 doublons détectés soit un taux de réussite de 95,5%, la distance de Jaro seule (0) donne le moins bon résultat.

Enfin pour l’algorithme IS, le choix du paramétrage est plus complexe car on peut choisir entre 6 indices de similarités, la longueur des Grammes (0 = mot à 5), l’inversion ou non des grammes et une distance maximum de recherche des grammes communs.
Pour la distance maxi, j’ai laissé à -1 (pas de limite de distance) car elle fournit les meilleurs résultats dans cet exemple et la recherche de grammes inversés donne ici de moins bons résultats.

J’ai donc joué sur le reste des paramètres (type d’indice et longueur des grammes) et les résultats sont synthétisés ici :

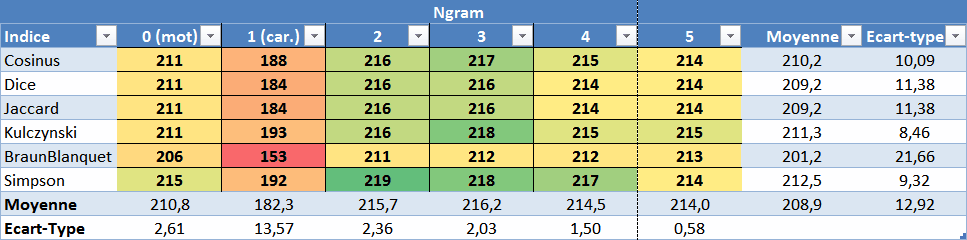
Les unigrammes (1) ont les moins bon résultats, la variabilité des résultats entre les indices diminue avec la longueur des grammes, les trigrammes et Simpson ont en moyenne les meilleurs résultats.

Pourcentage de réussite des indices en fonction de la longueur des grammes :

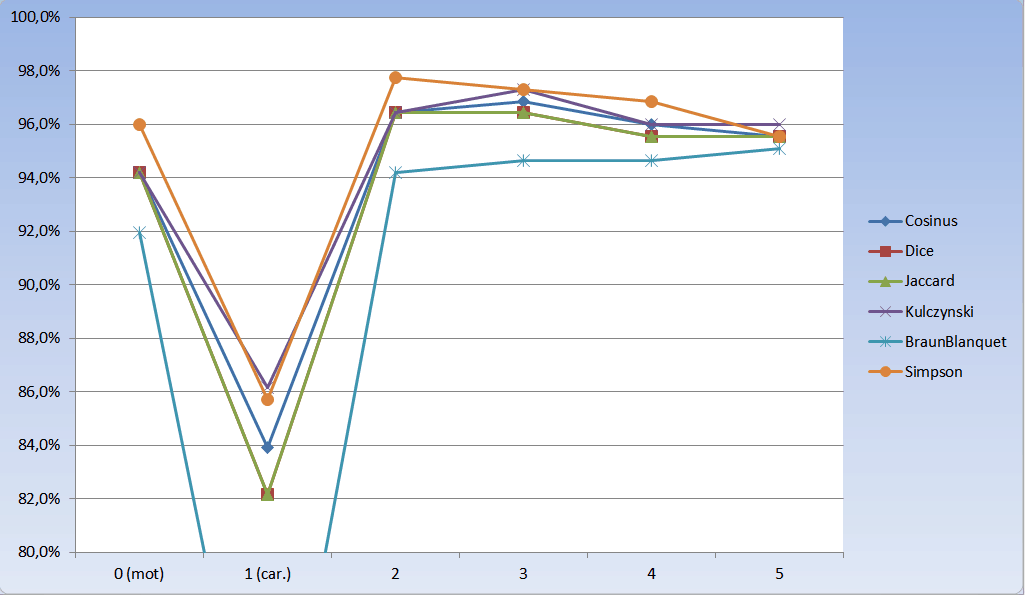
Finalement, l’indice de Simpson avec des bigrammes donne ici le meilleur résultat : 219 doublons détectés soit 97,8% de réussite !

Le tableau suivant indique le nombre de doublons détectés par position des résultats hormis le Top 1. Par exemple, 18 nouvelles bonnes détections faites par DL dans les Top 2 des résultats et Simpson en détecte 4 soit 223 détections cumulées (Top 1 et Top 2) sur 224 !.

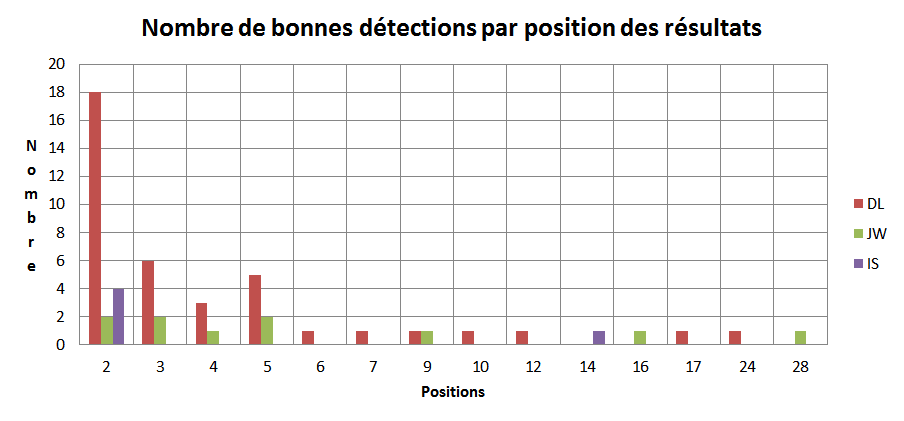
Après avoir vu rapidement la capacité des indices à détecter les vrais doublons, il faut vérifier leur capacité à être discriminant entre les restaurants et compter les éventuels ex aequo.
Imaginez un algo qui retourne un indice identique pour tous les restos : Ses résultats seraient parfaits mais pour chaque restaurant on aurait 223 restaurants détectés dans le Top 1 !

Via une requête, j’ai donc calculé la position absolue du vrai doublon pour chaque algorithme et chaque ligne. Des ex aequo sont présents si la position absolue est supérieure au classement.

JW n’est affecté qu’une fois par un ex aequo et ceci pour un classement du vrai doublon en 28ème position.
IS en a obtenu un seul sur un Top 1 et DL a eu 13 fois un ou plusieurs ex aequo.

Conclusion
Dans cet exemple, l’indice de Simpson a détecté le plus de doublons dans le Top 1 (219 sur 224) et 223 dans le Top 2 des résultats.
Si vous le souhaitez, vous pouvez ajouter vos propres résultats de vos algorithmes en commentaire du billet.

@+

Philippe