J’ai récement traduit l’article Implémenter un Voxel Cone Tracing, qui présente quelques difficultés techniques pour ceux qui ne sont pas habitués avec les concepts présentés dans cet article. Ce billet de blog à pour objectif de présenter ces concepts.

Quelques définitions

Illumination globale

Les techniques d’illuminations globales (GI) visent à améliorer le rendu d’une scène 3D, en prenant en compte aussi bien la lumière directe (les sources de lumières qui éclairent les objets) que la lumière indirecte (réflexion de la lumière sur les objets, qui éclaire d’autres objets). Ces techniques permettent d’obtenir des rendus réalistes, au prix d’un temps de calcul relativement long (parfois trop pour être compatible avec du rendu en temps réel). Un domaine de la recherche actuelle vise à développer de nouveaux algorithmes d’illumination globale compatible avec le temps réel (jeux 3D).

(source : Wikip̩dia РIllumination globale)

Illumination indirecte

Dans l’illumination directe (à gauche sur l’illustration suivante), la lumière provenant d’une source est directement réfléchie sur une surface, puis renvoyé vers la caméra. C’est le modèle classique de calcul de la lumière en 3D, que l’on retrouve par exemple dans le modèle de Phong. La lumière est alors décomposée en plusieurs composantes : la lumière ambiante (qui représente une illumination globale constante), la lumière diffuse (qui représente une diffusion de la lumière sur la surface) et la lumière spéculaire (qui représente une réflexion sur la surface).

(Source : Real-Time Global Illumination for Point Cloud Scenes)

Dans l’illumination indirecte, on considère que chaque surface qui reçoit de la lumière va à son tour en renvoyer. Il n’y a donc plus qu’une seule source de lumière, mais une infinité, correspondant à chaque surface qui renvoie de la lumière. Pour réaliser le rendu d’une scène, il faut donc procéder de la façon suivante :

1. pour chaque surface S1 visible par la caméra ;
2. pour chaque surface S2 visible depuis la surface S1 ;
3. calculer la lumière reçue par la surface S2 provenant de la source ;
4. calculer la lumière renvoyée par la surface S2 vers la surface S1 ;
5. calculer la lumière reçue par la surface S1 provenant de la surface S2 ;
6. calculer la lumière totale renvoyée par la surface S1 vers la caméra.

Chaque étape doit prendre en compte plusieurs paramètres. Pour (3), il faut par exemple prendre en compte la distance entre la source et la surface S2 et l’atténuation de la lumière en fonction de la distance. Pour (4), il faut prendre en compte les caractéristiques de la surface et sa capacité à réfléchir la lumière. Pour (5), il faut prendre en compte la distance entre les surfaces S1 et S2 et l’angle d’incidence. Pour (6), les capacités de réflexion de la surface S1 et la distance entre la surface S1 et la caméra.

Cette première approche simple peut largement être améliorée (et complexifiée), en prenant en compte par exemple que la lumière peut se réfléchir plusieurs fois sur des surfaces avant d’atteindre la caméra (particulièrement important lorsque les surfaces sont très réfléchissantes, comme du verre ou du métal poli), de la diffusion de la lumière dans le brouillard ou la poussière (lumière volumétrique, éclat lumineux), la présence de plusieurs sources lumineuses (voir des milliers de sources lumineuses dans le cas de particules incandescentes).

Lancé de rayons

Il existe plusieurs techniques de « lancés ». Elles reposent sur l’idée que la lumière est constituée de rayons qui vont partir de des sources lumineuses, se réfléchir, diffuser et réfracter sur les différentes surfaces (chaque surface pouvant renvoyer plusieurs rayons), puis atteindre la caméra. Dans les techniques de photon mapping, on part des sources lumineuses, on émet des rayons et on les suit jusqu’à la caméra (cette technique est décrite dans un autre article du blog de Simon et fera l’objet d’une traduction). Dans les techniques de lancé de rayons, on part de la caméra, on lance un rayon pour chaque pixel de l’image finale et l’on remonte jusqu’aux sources de lumière (illustration suivante).

(Source : Wikip̩dia РRaytracing)

Dans la technique du lancé de cônes (Cone Tracing), présentée dans l’article traduit, on remplace simplement les rayons par des cônes pour le calcul de l’illumination.

Occlusion ambiante

Cette technique fera également l’objet de plusieurs traductions du blog de Simon, je la détaillerai à ce moment là.

Simplement pour comprendre l’idée générale : lorsque deux surfaces sont proches (dans une fissure, un trou), la lumière indirecte diminue fortement et l’on observe des ombres douces. Plus les surfaces sont proches et fermées, plus l’ombrage sera important. L’illustration suivante représente la même scène sans (en haut) et avec l’occlusion ambiante (en bas). Remarquez en particulier l’ombre dans l’angle du mur et du sol et entre la sphère dans l’image du bas.

Cette technique améliore fortement la qualité du rendu et commence à être très utilisée dans les jeux. Un de ses points forts est que pour un objet statique (ou peu dynamique), l’occlusion ambiante ne varie pas (ou peu) et il est possible de la pré-calculer, le résultat étant mis dans une texture. Il suffit ensuite d’appliquer la texture sur l’objet lors du rendu, comme n’importe quelle autre texture.

Il existe plusieurs algorithmes de calcul de l’occlusion ambiante, mais pour comprendre le principe, voyons un exemple simple représenté dans l’illustration suivante. Pour chaque point d’une surface, on va lancer un nombre fixé de rayons qui vont parcourir une distance fixée aussi dans toutes les directions. On compte ensuite le nombre de rayons qui ne rencontrent pas une autre surface et on calcul le rapport entre le nombre de rayons ayant rencontrés une surface et le nombre de rayons lancés. Ainsi, dans l’illustration suivante, pour le point A, sur les six rayons lancés, aucun ne rencontre de surfaces, le rapport est de 0/6 = 0 %. Pour le point B, seul quatre rayons ne rencontrent pas de surfaces sur les six lancés, le rapport est de 4/6 = 66 %. Pour le point C, deux rayons ne rencontrent pas de surfaces, le rapport est de 2/6 = 33 %.

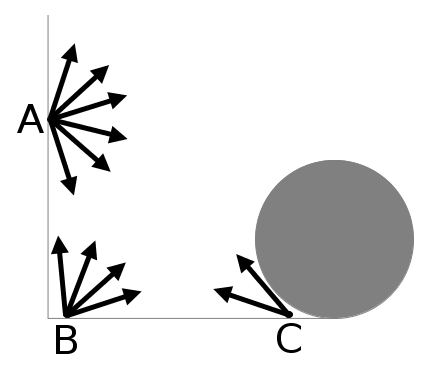
Il suffit ensuite d’atténuer la lumière pour chaque point en fonction du rapport calculé. Plus le rapport est proche de 0 %, plus la surface sera sombre et plus le rapport est proche de 100 %, plus la surface est claire.

Pour obtenir un bon rendu, on pourra augmenter le nombre de point et le nombre de rayons lancés, mais l’impact sur les performances sera important.

Partitionnement de l’espace

Voxel

Le principe des voxels est relativement simple : ils sont l’équivalent en 3D des pixels pour la 2D. Un exemple bien connu d’utilisation des voxels est le jeu Minecraft, dans lequel chaque élément (terrain, objets) sont représentés par des cubes.

(Source : Wiki̩pdia РMinecraft)

Les voxels sont particulièrement gourmand en termes de performances et sont encore peu utilisés pour les jeux vidéos. Ils sont particulièrement adaptés pour le rendu de volumes transparents (verre, liquide, fumée, nuage) ou de géométries très complexes (pour le rendu d’un mesh complexe, une approche utilisant une version low poly du mesh et une texture des Displacement/Normal/Bump mapping).

Octree

Un octree est une structure permettant de partitionner l’espace dans un arbre, permettant par exemple de faciliter la recherche d’un élément par rapport à sa position 3D. La construction d’un tel arbre est simple : à chaque itération, le cube représentant une partie de l’espace est divisé en 8 cubes.

(Source : GPU Gems 2 – Octree Textures on the GPU)

L’intérêt des octrees avec les voxels est que l’on va pouvoir utiliser une structure « creuse » : les zones qui sont vides ne seront pas divisées en cubes plus petits, simplifiant ainsi les algorithmes de recherche et la mémoire.