Ici je suppose que ma plaque fait 10 mètres de long sur 6 de large , que je connais la température sur cette plaque sur 8 points. Pour avoir une idée de comment se propage la température sur cette plaque je dois donc interpoler ces points.

Commencons par créer notre figure et notre dataset:

%% Figure sans menu et sans numéro :
figure(‘name’,’Interpolation avec TriScatteredInterp’,’numbertitle’,’off’,’menubar’,’none’)

%% Température connue sur 8 points
x = [0 1 2 4 7 8 9 10]'; % longueur allant de 0 à 10
y = [0 3 5 2 1.5 1 1 6]'; % largueur allant de 0 à 6
temperature = [12 20 98 45 12 0 14 60]'; % 8 valeurs de température

Ensuite créons notre maillage et notre interpolant :

%% Création du maillage : 1 point tous les 10 cm
[Xinterp,Yinterp] = meshgrid(min(x):0.1:max(x),min(y):0.1:max(y));

%% Création de l’interpolant
F = TriScatteredInterp(x,y,temperature);
% Evaluons cet interpolant en (Xinterp,Yinterp).
% Les valeurs correspondantes à ces points est Zinterp:
Zinterp = F(Xinterp,Yinterp);

A ce stage là Xinterp, Yinterp et Zinterp sont des matrices 61*101. Normal vu qu’il faut 61 bâtons tous les 10 cm entre 0 et 6 mètres et 101 bâtons espacés de 10 cm entre 0 et 10 mètres.
Toujours compliqué ces histoires de bâton et d’intervalles ,enfin bref.
Maintenant il ne nous reste plus qu’à s’occuper de la partie graphique.

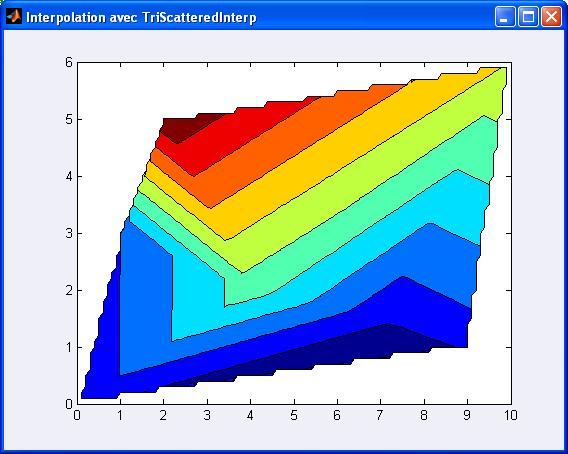
Un petit contouring pour commencer :

>> contourf(gca,Xinterp,Yinterp,Zinterp)

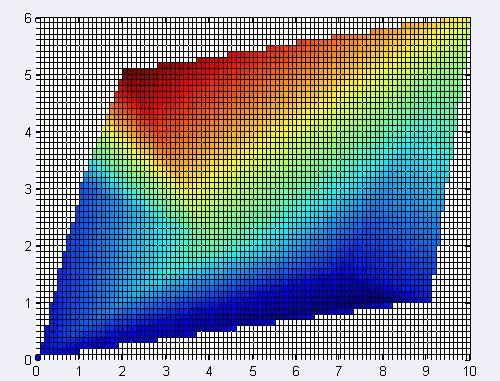
Un petit échiquier pour la route :

>> pcolor(gca, Xinterp,Yinterp,Zinterp);

on est bien d’accord on peut pas en rester là !
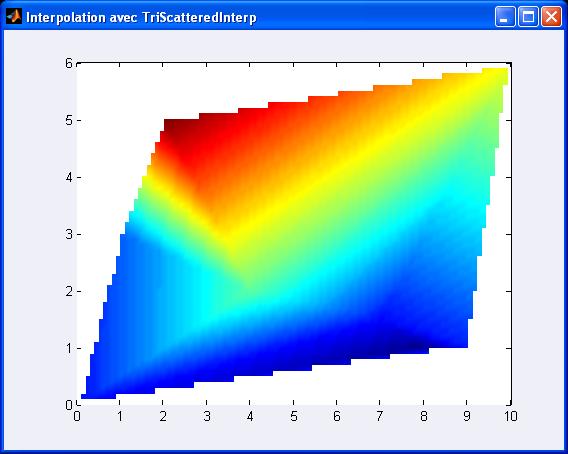
Du coup ce qu’on va faire c’est qu’on va colorer chaque cellule par une interpolation bilinéaire des couleurs des 4 cotés en utilisant toutes les valeurs de Zinterp.
Rien de compliqué :

>> shading(gca,’interp‘)

A noter pour les geeks qu’on aurait eu le même résultant en mettant au pcolor les propriétés facecolor à interp et EdgeColor à none. Beh oui car comme tout geek qui se respecte , on sait que par défaut notre pcolor a son facecolor à flat et son EdgeColor à [0 0 0]

Beaucoup mieux non?! Bon beh pour finir en beauté on va faire un peu de design.

%% Colorbar avec un titre
col = colorbar;
set(get(col,’title’),’String’,'[degrés]’,’fontweight’,’bold’)
set(gca,’tickdir’,’out’,’fontweight’,’bold’)

%% Design axes
xlabel(‘Longueur (m)’)
ylabel(‘Largeur (m)’)
title(‘Température sur une plaque de 10*6 m’)
box(‘off’)
shg % me fait apparaitre ma figure

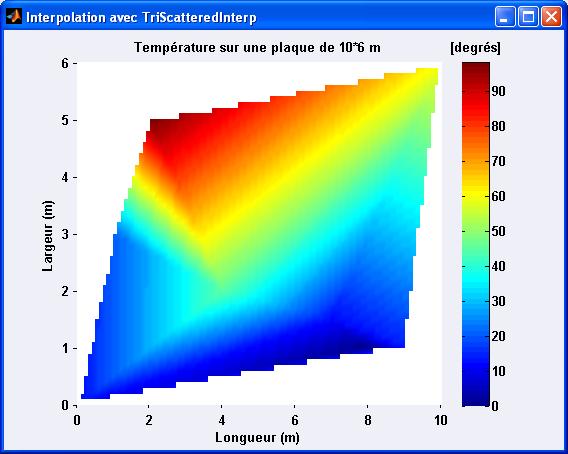
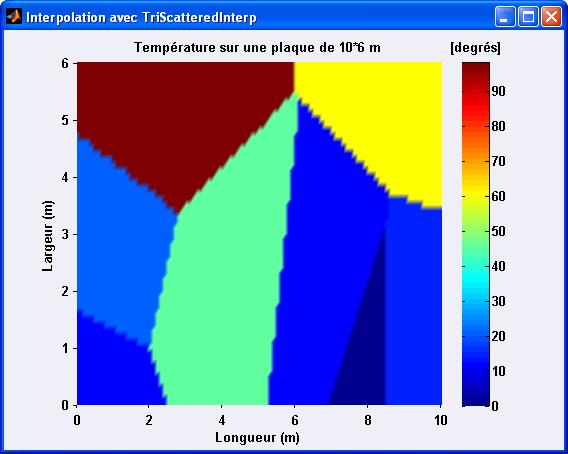
Ce qui nous donne en image finale :

On a bien la température la plus chaude (98 degrés) au point (2,5) .
Pour s’en rassurer il suffirait de taper F(2,5) . Pour connaitre la température en (3,3) par exemple , il suffit de taper F(3,3) qui retourne 56.5 degrés.

Et que vaut la température au point (0,1) ? un NaN , normal vu qu’on n’a pas de valeur interpolée pour ce point. Pour ce cas là on aurait besoin que notre interpolant recouvre toute la plaque. Pareil ce n’est pas compliqué ! Si on veut couvrir tout l’ensemble de notre plaque il faut dire à TriScatteredInterp qu’on veut utiliser la méthode ‘nearest’. Par défaut la méthode est Linear. L’autre méthode est Natural.

>> F = TriScatteredInterp(x,y,temperature,’nearest’);

Et maintenant on est content de avoir que sur notre plaque en (0,1) , il fait 20.1 degrés !

Bon beh voilà pas compliqué , on aurait pu augmenter ou réduire notre gridding qui était de 10 cm , on aurait pu aussi faire une interpolation linéaire avec une extrapolation au voisin le plus proche , c’est à dire enlever les NaN en sortie de notre interpolant , on aurait pu à la fin se faire plaisir en changeant la colormap par défaut par colormap(flipud(hot)) … Mais bon ce n’était pas le but du billet , je voulais juste vous montrer la simplicité de cette méthode.