Un système d’information géographique (SIG ou GIS en anglais pour geographical information system, aussi appelé SIRS pour système d’information à référence spatiale) est constitué de type de données et méthodes permettant d’établir des plans et des cartes pour traiter différents problèmes relatifs aux données spatiales et planaires. Les SIG sont aujourd’hui largement intégrés aux SGBDR et permettent des manipulations via des requêtes écrites en langage SQL.
Ceci est la première partie de cet article sur les SIG avec SQL dans les SGBDR.
L’intérêt de l’utilisation des SIG dans les bases de données repose sur différents éléments
tels que :
- la possibilité d’exploiter de très grands volumes de données géographiques, y compris
spatio-temporelles (par exemple un historique de la pluviométrie des cours d’eau) ; - la fiabilité et la sécurisation des données qu’apporte naturellement le SGBD, notamment pas la gestion des privilèges;
- la possibilité de poser des contraintes spatiales et spatio-temporelles afin de garantir
la qualité des données; - et l’indexation rendue nécessaire pour assurer de bonnes performances aux divers
traitements, notamment de restitution de l’information.
Il existe deux standards en matière de spécification des objets spatiaux : la norme SQL et la spécification de l’Open Geospatial Consortium (OGC), une organisation ouverte de standardisation des formats et méthodes de manipulation des données spatiales.
NOTA : une partie de cet article est extraite du chapitre 8 du Livre « SQL (3e édition) », collection Synthex – Pearson Education 2010 – Auteurs : Frédéric Brouard, Christian Soutou, Rudi Bruchez
Vous trouverez de nombreux autres commentaires sur ce sujet dans cet ouvrage.
0 – Introduction
La norme SQL est bien plus détaillée dans sa description des types et des méthodes que ne l’est la spécification de l’OGC. En revanche la spécification OGC, standardisée, est plus réaliste et plus simple d’implémentation.
La spécification OGC « Simple feature for SQL », propose un ensemble d’éléments pour standardiser le stockage et la gestion des données géographiques dans les SGBDR. Ce standard, bien que plus simple que la norme SQL, est suffisamment complet et détaillé, à la fois pour SQL et les couches objets OLE/COM des API pour réaliser tous types de traitements. C’est une solution intéressante pour résoudre en partie les problèmes liés à l’interopérabilité des informations géographiques. C’est pourquoi la majorité des SGBDR ont opté pour ce standard et non pour la norme SQL.
Nous allons présenter les spécification de l’OGC et comparer ce qui se fait sur les deux SGBDR que sont PostGreSQL et Microsoft SQL Server 2008.
1 – Type SQL pour les objets spatiaux
SQL propose comme élément générique des objets spatiaux les types GEOMETRY et GEOGRAPHY . Le premier est consacré à la géométrie euclidienne tandis que le second propose de travailler sur le géoïde terrestre, ce qui impose un référentiel spatial de projection (SRID).
2 РTypes des donn̩es spatiales
« Simple Feature for SQL » propose une hiérarchie de types géométriques et des méthodes associées, plus simple que celle proposée par SQL. Voici son arborescence :
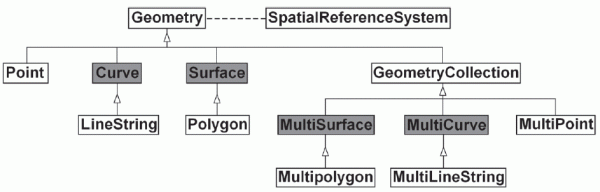
Figure 1 – Hiérarchie des types de données géométrique de l’OGC – en gris foncé, les types non instanciables.
Le type générique Geometry possède les sous-types point (Point ), courbe (Curve), surface (Surface) ou collection géométrique (GeometryCollection ).
Une surface peut être initiée par un polygone (Polygon) de même qu’une courbe peut être initiée par une ligne brisée (LineString ).
Une collection géométrique (GeometryCollection) est un objet géométrique contenant différents objets géométriques hétérogènes.
Multipoint (MultiPoint ), multicourbe (MultiCurve) et multisurface (MultiSurface) sont utilisés pour gérer des collections d’objets homogènes, respectivement ensemble de points, de courbes ou de surfaces.
Une multisurface peut être initiée par un multipolygone (MultiPolygon ) et une multicourbe par une multiligne brisée (MultiLineString ).
Certains types ne sont pas instanciables. Ils sont déduits d’autres objets. Par exemple, la courbe (Curve) est définie par une ligne brisée (LineString) à l’échelle désirée (fractale). De même pour la surface (Surface) qui est déduite de l’application d’une transformation d’un polygone (Polygon). Il en est de même pour les types multisurface et multicourbe.
Figures 2 :
a à c : Point (Point), ligne brisée, (LineString) et polygone, (Polygon).
d à f : Multipoint (Multipoint), multiligne brisée (MultiLineString) et multipolygone (MultiPolygon).
g : Collection géométrique (GeometryCollection).
Tout objet géométrique doit être référencé par un identifiant spatial (SRID ou Spatial Reference System Information) qui correspond à une cartographie spécifique de l’ellipsoïde terrestre et décrit l’espace de coordonnées dans lequel on travaille.
3 РRepr̩sentation logique des donn̩es g̩om̩triques
Il existe principalement trois modes de représentation des données géométriques. Le mode dit « spaghetti », le mode graphe et le mode topologique. OGC implémente le mode spaghetti.
Le mode spaghetti propose de décrire chaque objet géométrique en toute indépendance des autres objets qui composent un ensemble cohérent. Ainsi, la représentation des pays de l’Europe serait dans ce mode un assemblage de polygones strictement indépendants.
Si ce mode est d’une grande simplicité de mise en oeuvre, il possède l’inconvénient que les relations topologiques entre objets doivent être calculées à la demande. Pire, sans contrôles tels que la mise en oeuvre de contraintes, il est possible que deux pays voisins n’aient en définitive aucune frontière commune du fait d’une erreur de saisie. De la même manière, rien n’interdit dans un tel modèle de situer une ville (donc un point géométrique) en dehors des limites géométriques d’un pays (un polygone). Enfin, le modèle est fortement redondant puisque les frontières entre régions voisines sont décrites deux fois.
Si les éditeurs de SGBDR ont pour la plupart retenu le mode spaghetti c’est parce qu’il possède deux avantages : la facilité de mise à jour et la facilité d’indexation des données, car n’oublions pas que l’intérêt des serveurs de bases de données et de permettre des traitements très rapides des données grâce à une bonne indexation !
4 РIdentificateur de r̩f̩rence spatiale (SRID)
Tout objet géométrique doit être référencé par un identifiant spatial (SRID ou Spatial Reference System Information) qui correspond à une cartographie spécifique de l’ellipsoïde terrestre et décrit l’espace de coordonnées dans lequel on travaille.
L’identificateur de référence spatiale (ou SRID, pour Spatial Reference System Information) permet de savoir à quel système de coordonnées on se réfère et de connaître la mesure étalon des distances (mètre, pied…).
En fait, la Terre n’étant pas parfaitement sphérique, mais légèrement aplatie aux pôles, les projections des cartes doivent tenir compte de ce fait, et c’est donc un géoïde elliptique qui est la représentation la plus approchante de notre globe terrestre. Pour autant, il n’existe pas une seule forme admise de représentation, mais bien plusieurs, toutes basées sur une ellipse, mais dont les points de référence peuvent être différents.
Pour information, disons que grosso modo la Terre mesure quelque 6 380 km de rayon à l’équateur et 6 360 km aux pôles, mais cette paille de 20 km peut devenir une poutre si elle n’est pas correctement prise en compte.
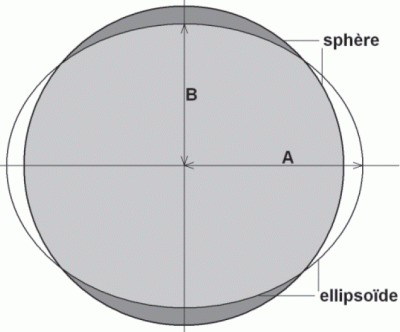
Figure 3 – Représentation de l’ellipsoïde terrestre avec demi-grand axe A et demi-petit axe B.
Dans les différents systèmes de coordonnées, la distance entre deux objets peut varier, même si les objets ont des coordonnées identiques, car les distances planaires et géodésiques suivent deux géométries différentes. Il ne sera donc pas possible d’appliquer différentes fonctions de calcul si les références spatiales des objets ne sont pas identiques.
Les éléments d’une référence comportent le code et le nom de la référence et des données techniques qui sont : les données mathématiques de l’ellipsoïde de référence (la Terre n’étant pas parfaitement ronde), un méridien pour origine des longitudes et l’unité d’angle. L’unité de mesure des distances doit aussi être connue.
Le référentiel actuel en France est connu sous le nom de code RGF93 (abréviation de réseau géodésique français 1993). C’est le système géodésique officiel en France depuis le 1er janvier 2001 pour tous les travaux de nature publique de plus de 1 hectare, ou dont la plus grande longueur est supérieure à 500 m (décret du 26 décembre 2000 modifié par le décret 2006-272 du 3 mars 2006). Ses données techniques sont les suivantes :
GEOGCS[«RGF93»,
DATUM[«Reseau Geodesique Francais 1993»,
ELLIPSOID[«GRS 1980», 6378137, 298.257222101]],
PRIMEM[«Greenwich», 0],
UNIT[«Degree», 0.0174532925199433]]
Notez l’imbrication des différents éléments.
Pour cette référence, les données numériques de l’ellipsoïde sont les suivantes : demin-grand axe (A = 6378137) et inverse de l’aplatissement (1/F = 298,257222101). Ces deux données permettent de retrouver la 3e donnée importante qu’est le demi-petit axe B, par la formule : B = A – A * F, soit 6356454,32.
Le méridien de référence est celui de Greenwich, l’unité angulaire est le degré, c’est-à -dire 0,0174532925199433 radian.
Pour le monde entier, on utilise un autre système de référence, le WGS 84 (World Geodetic System 1984), dont les données sont les suivantes :
GEOGCS[«WGS 84»,
DATUM[«World Geodetic System 1984»,
ELLIPSOID[«WGS 84», 6378137, 298.257223563]],
PRIMEM[«Greenwich», 0],
UNIT[«Degree», 0.0174532925199433]]
Cette façon particulière de présenter les données techniques d’un référentiel spatial (aux indentations près) n’a rien de hasardeux et s’appelle le format Well Known Text – nous en discuterons un peu plus loin.
Les SRID (identifiants numérique sous forme d’entier) de ces deux référentiels sont communément les 4171 ou 4965 (RGF93) et 4326 (WGS 84).
Pour la plupart de ces référentiels, les distances sont calculées en mètres, mais certaines anciennes mesures furent utilisées. Les principales figurent ci-après.
Clarke’s foot : 0,304797265 m
foot : 0,3048 m
German legal metre : 1,000013597m
Indian foot : 0,30479951m
US survey foot : 0,30480061m
Vous trouverez toutes les références exprimées dans tous les formats à l’url : http://spatialreference.org/
Par convention, la plupart des SGBD autorisent de ne pas mentionner le SRID pour les données strictement euclidiennes. Dans ce cas, il s’agit de géométrie et non plus de géographie et le SRID à pour valeur généralement 0 ou –1.
NOTA : la plupart des SRID ont été recensés par un organisme aujourd’hui disparu, l’EPSG (European Petroleum Survey Group). Ne soyez donc pas étonnés de retrouver parfois cet acronyme dans les différentes références présentées par les éditeurs de SGBDR.
ATTENTION : PostGreSQL est actuellement très limité au niveau des types GEOGRAPHY car un seul référentiel géodésique est accepté le SRID 4326 (WGS 84)
5 – Expression des valeurs
Nous avons vu que les éditeurs de SGBDR ont opté pour décrire les objets suivant le mode spaghetti. Pour autant il faut s’entendre sur le « format » de la description…
Exprimer une valeur pour un type spatial se fait de deux façons, soit en Well Known Text (WKT en abrégé, texte bien connu en français), c’est-à -dire par description de l’entité sous forme littérale, soit en Well Known Binary (WKB en abrégé – binaire bien connu), c’est-à -dire sous la forme d’une chaîne hexadécimale.
Bien entendu, il existe des méthodes pour passer de l’un à l’autre.
Comme tout objet spatial possède un SRID, celui-ci doit être passé en argument après la description géométrique de l’objet. Il s’agit d’un entier.
La syntaxe de l’expression d’une valeur d’objet spatial est alors la suivante :
' <représentation> ' [ , <SRID> ]
<représentation> ::= <représentation_WKT>
| <représentation_WKB>
Nous allons nous intéresser à la forme la plus compréhensible pour nous, c’est-à -dire au WKT ou Well Known Text. Dans ce format, la chaîne de caractères commence par décrire sous forme littérale et majuscule le sous-type parmi POINT, LINESTRING, POLYGON, MULTIPOINT, MULTILINESTRING, MULTIPOLYGON ou GEOMETRYCOLLECTION. Puis les données techniques indicatives de la forme suivent entre parenthèses ou bien le mot clef EMPTY.
Syntaxe :
<représentation_WKT> ::=
' <forme> { ( <données_techniques> )
| EMPTY } '
<forme> ::= POINT
| LINESTRING
| POLYGON
| MULTIPOINT
| MULTILINESTRING
| MULTIPOLYGON
| GEOMETRYCOLLECTION
Les données techniques diffèrent suivant la forme géométrique concernée.
5.1 – Point :
<données_techniques> ::= <X> <Y>
Ou X et Y sont les abscisse et ordonnée du point sous forme de réels. Notez l’espace
séparateur des deux coordonnées.
Exemple 1
'POINT(33.3 22.2)'
NOTA : on peut associer à un point une troisième coordonnée Z (élévation) et une mesure M. Par exemple, M peut être une mesure de pluviométrie, d’ensoleillement, de limnimétrie… Dans ce cas, on peut ajouter directement les coordonnées Z ou Z + M à la suite des coordonnées X et Y, ou bien préciser dans la partie littérale quelles coordonnées supplémentaires doivent figurer.
Exemple 2
'POINT(1 2 3 4)'
'POINT Z (1 2 3)'
'POINT M (1 2 4)'
'POINTZM (1 2 3 4)'
5.2 РLigne bris̩e (LineString) :
<données_techniques> ::= <X1> <Y1> , <X2> <Y2> [ , <X3> <Y3> [ , … ] ]
Ou Xn et Yn sont les abscisses et ordonnées des points par lesquels passe la ligne brisée. Notez la virgule, habituel séparateur des listes d’éléments en SQL.
Exemple 3
'LINESTRING(33.3 22.2, 36.3 41.2)'
5.3 – Polygone (Polygon) :
<données_techniques> ::= ( <X1> <Y1> , <X2> <Y2> , <X3> <Y3> [ , <X4> <Y4> [ , … ] ], <X1> <Y1> )
Ou Xn et Yn sont les abscisses et ordonnées des points par lesquels passe le périmètre du polygone. Notez que le polygone doit comporter au moins 3 points différents et que le premier est répété en fin de liste pour fermeture. Enfin, l’ensemble des points périmétriques est spécifié entre parenthèses.
Exemple 4
'POLYGON((33.3 22.2, 41.0 25.12, 44.3 51.2, 33.3 22.2))'
'POLYGON((0 0, 3 0, 3 3, 0 3, 0 0),(2 2, 2 1, 1 1, 1 2, 2 2))'
Exemple 5 – trois polygones (sous MS SQL Server)
SET @geo1 = 'POLYGON((25.1 22.2, 41.0 25.12, 44.3 51.2, 25.1 22.2))';
SET @geo2 = 'POLYGON((36.3 25.2, 20.0 25.12, 41.3 46.2, 21.6 48.1, 36.3 25.2))';
SET @geo3 = 'POLYGON((20 20, 32 20, 32 32, 20 32, 20 20), (28 28, 28 24, 24 24, 24 28, 28 28));
SELECT @geo1
UNION ALL
SELECT @geo2
UNION ALL
SELECT @geo3;
5.4 – Multi point (MultiPoint) :
<données_techniques> ::= ( <point1> ) [ , ( <point2> ) [ , … ] ]
Exemple 6
'MULTIPOINT ((25.2 12.8), (35.3 11.4))'
5.5 РMulti ligne bris̩e (MultiLineString) :
<données_techniques> ::= ( <MultiLineString1> ) [ , ( <MultiLineString2> ) [ , … ] ]
Exemple 7
'MULTILINESTRING ((25.1 30.2, 40.8 12.6), (44.1 42.2, 21.6 14.9, 18.0 22.9))
‘
5.6 – Multi polygone (MultiPolygon) :
<données_techniques> ::= ( <Polygone1> ) [, ( <Polygone2> ) [ , … ] ]
Exemple 8
'MULTIPOLYGON (((25.1 35.2, 10.9 15.1, 10.0 10.9, 25.1 35.2)), ((10.2 10.9, 15.8 28.4, 31.0 22.1, 10.2 10.9)))'
5.7 РCollection g̩om̩trique (GeometryCollection) :
<données_techniques> ::= ( <ObjetGeometrique1> ) ] [, ( <ObjetGeometrique2> ) [ , … ] ]
Exemple 9
'GEOMETRYCOLLECTION(POLYGON((5 5, 10 5, 10 10, 5 5)),
POINT(10 10),
MULTIPOLYGON (((15.1 15.2, 6.9 15.1, 10.0 10.9, 15.1 15.2)),
((9 7, 12 16, 13 14, 9 7))),
LINESTRING(7 10, 12 14, 14 5, 9 9))'
6 РM̩thodes
Voici maintenant les méthodes proposées pour manipuler les objets.
Nous présenterons d’abord les constructeurs de types, puis les méthodes génériques et enfin les méthodes spécifiques.
NOTA : Bien que la plupart des méthodes soient conforment au standard OGC, PostGreSQL a adopté le style SQL normatif de notation des méthodes, tandis que Microsoft SQL Server à adopté son propre style proche de celui d’OGC.
Pour PostGreSQL, les méthodes sont préfixées ST_ (les lettres S et T en majuscule suivies du blanc souligné), tandis que SQL Server les préfixe avec les lettres ST en majuscule. De plus les méthodes MS sont sensible à la casse du fait du codage .net.
Ainsi la méthode IsEmpty() qui permet de savoir si une instance géométrique est vide ou non s’appelle ST_IsEmpty() sous PostGreSQL et STIsEmpty() sous MS SQL Server.
6.1 – Constructeur de types
Un constructeur de types permet d’initialiser un objet spatial en créant sont instance avec une définition littérale ou binaire de l’objet à créer.
Il existe différentes méthodes de construction des types spatiaux, en commençant par les méthodes généralistes :
GeomFromWKB (awkb BINARY LARGE OBJECT(ST_MaxGeometryAsBinary), SRID INTEGER) : Geometry
Crée une instance d’un type Geometry par Well Known Binary avec un SRID.
GeomFromText (awkt CHARACTER LARGE OBJECT(ST_MaxGeometryAsText), SRID INTEGER) : Geometry
Crée une instance d’un type Geometry par Well Known Text avec un SRID.
Il existe aussi des constructeurs plus spécialisés par types d’objet, aussi bien pour le format WKT que pour le format WKB :
Format WKT Format WKB
------------------ -----------------
PointFromText PointFromWKB
LineFromText LineFromWKB
PolyFromText PolyFromWKB
MPointFromText MPointFromWKB
MLineFromText MLineFromWKB
MPolyFromText MPolyFromWKB
GeomCollFromText GeomCollFromWKB
Exemple 10 – Création d’objets géométriques (avec PostGreSQL / PostGIS)
CREATE TABLE SIG.T_GEO (GEO_NOM VARCHAR(16), GEO_OBJET GEOMETRY);
INSERT INTO SIG.T_GEO (GEO_NOM, GEO_OBJET)
VALUES ('Un point', ST_GeomFromText('POINT(123 456)'));
INSERT INTO SIG.T_GEO (GEO_NOM, GEO_OBJET)
VALUES ('Une ligne', 'LINESTRING(96 352, 136 212, 77 401)');
SELECT *, ST_AsText(GEO_OBJET) AS WKT
FROM SIG.T_GEO;
GEO_NOM GEO_OBJET WKT
---------- ----------------------------------- ---------------------------------
Un point 01010000000000000000C05E40000000… POINT(123 456)
Une ligne 01020000000300000000000000005840… LINESTRING(96 352,136 212,77 401)
Exemple 11 РIdem pr̩c̩dent (avec MS SQL Server)
CREATE TABLE SIG.T_GEO (GEO_NOM VARCHAR(16), GEO_OBJET GEOMETRY);
INSERT INTO SIG.T_GEO (GEO_NOM, GEO_OBJET)
VALUES ('Un point', geography::STGeomFromText('POINT(12.33 44.26)'));
INSERT INTO SIG.T_GEO (GEO_NOM, GEO_OBJET)
VALUES ('Une ligne', 'LINESTRING(96 352, 136 212, 77 401)');
SELECT *, GEO_OBJET.STAsText() AS WKT
FROM SIG.T_GEO
GEO_NOM GEO_OBJET WKT
---------- ----------------------------------- --------------
Un point 0x00000000010C295C8FC2F5A82840E1… POINT (12.33 44.26)
Une ligne 0x000000000104030000000000000000… LINESTRING (96 352, 136 212, 77 401)
6.2 РTranstypage des types g̩om̩triques
Bien entendu il est possible d’obtenir la définition WKT ou WKB d’un objet à l’aide des méthodes suivantes :
AsBinary (G Geometry ) : BINARY LARGE OBJECT(ST_MaxGeometryAsBinary)
Renvoie le format WKB de l’objet géométrique;
AsText (G Geometry ) : CHARACTER LARGE OBJECT(ST_MaxGeometryAsText)
Renvoie le format WKT de l’objet géométrique;
6.3 РM̩thodes communes
Ces méthodes sont des méthodes générales applicables à n’importe quel type de données spatiales.
Méthode | Description
---------------------------|---------------------------------------------------------
Boundary() : Geometry |Retourne l’objet bornant (frontière) l’objet considéré
|(périmètre au plus près)
---------------------------|---------------------------------------------------------
Dimension() : Integer |Retourne la dimension spatiale de l’objet de 0 à 2 (un
|point étant de dimension 0, une ligne 1, un polygone 2…)
---------------------------|---------------------------------------------------------
Envelope() : Geometry |Renvoie un objet polygone représentant l’enveloppe
|polygonale (rectangulaire si géométrie) minimale dans
|laquelle rentre l’objet. Ce polygone peut inclure les
|coordonnées Z et M si elles sont définies
---------------------------|---------------------------------------------------------
GeometryType() : String |Retourne le nom d’instance du type de l’objet (Point,
|LineString, Polygon…)
---------------------------|---------------------------------------------------------
SRID() : Integer |Retourne l’identifiant de la référence spatiale
---------------------------|---------------------------------------------------------
IsEmpty() : Integer |Renvoie 1 si l’objet est vide (EMPTY) sinon 0
---------------------------|---------------------------------------------------------
IsSimple() : Integer |Renvoie 1 si l’objet n’a aucun point tangent ou croisant
|un de ses autres points, sinon 0
---------------------------|---------------------------------------------------------
Is3D() : Integer |Renvoie 1 si l’objet a des coordonnées en Z (élévation),
|sinon 0
---------------------------|---------------------------------------------------------
IsMeasured() : Integer |Renvoie 1 si l’objet a des coordonnées en M (mesure),
|sinon 0
-------------------------------------------------------------------------------------
NOTA : pour les fonctions IsEmpty, IsSimple, Is3D et IsMesured, le type de retour est un entier, mais doit être interprété comme un booléen : 1 Vrai, 0 Faux.
Exemple 12 – avec MS SQL Server
CREATE TABLE SIG.T_GEOGRAPHY (GEO_NOM VARCHAR(24), GEO_OBJET geography);
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('Point', geography::STGeomFromText('POINT(3 3)', 4171) );
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('LineString', geography::STGeomFromText('LINESTRING(0 0, 3 3)', 4965));
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('Polygon', 'POLYGON((0 0 1, 3 0 2, 0 3 2, 0 0 1))');
SELECT GEO_NOM, GEO_OBJET.STDimension() AS dimension,
GEO_OBJET.STGeometryType() AS GeoType,
GEO_OBJET.STSrid AS SRID
FROM SIG.T_GEOGRAPHY;
GEO_NOM dimension GeoType SRID
---------- ----------- ------------ -----------
Point 0 Point 4171
LineString 1 LineString 4965
Polygon 2 Polygon 4326
Cet exemple montre l’utilisation des méthodes Dimension, GeometryType et SRID avec Microsoft SQL Server 2008.
Exemple 13 Рidem pr̩c̩dent avec PostGreSQL / PostGis
CREATE TABLE SIG.T_GEOGRAPHY (GEO_NOM VARCHAR(24), GEO_OBJET GEOGRAPHY);
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('Point', ST_GeomFromText('POINT(3 3)', 4326) );
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('LineString', ST_GeomFromText('LINESTRING(0 0, 3 3)', 4326));
INSERT INTO SIG.T_GEOGRAPHY
VALUES ('Polygon', 'POLYGON((0 0 1, 3 0 2, 0 3 2, 0 0 1))');
SELECT GEO_NOM, ST_Dimension(GEO_OBJET) AS dimension,
ST_GeometryType(GEO_OBJET) AS GeoType,
ST_Srid(GEO_OBJET) AS SRID
FROM SIG.T_GEOGRAPHY;
GEO_NOM dimension geotype srid
---------- ----------- --------------- -----------
Point 0 ST_Point 4326
LineString 1 ST_LineString 4326
Polygon 2 ST_Polygon -1
REMARQUE : Le type GEOGRAPHY de PostGreSQL/PostGis est sévèrement limité et les fonctions Dimension, GeometryType ou Srid sont inopérantes. Il faut donc passer par un type GEOMETRY qui ne permet pas de définir un autre SRID que le 4326.
Exemple 14 – avec MS SQL Server
CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('A', geometry::STGeomFromText('LINESTRING (0 0, 15 70, 25 70, 40 0,
31.42857 40, 8.57428 40 )', 0));
INSERT INTO SIG.T_GEOMETRY
VALUES ('B', geometry::STGeomFromText('LINESTRING (50 40, 50 0, 70 0, 82 5, 90 15, 90 25,
82 35, 70 40, 50 40, 50 70, 70 70, 80 65,
83 55, 80 45, 70 40)', 0));
SELECT 'Lettre : ' + GEO_NOM AS NOM, GEO_OBJET.STAsText() AS Geo_Objet
FROM SIG.T_GEOMETRY
UNION ALL
SELECT GEO_NOM + ' - enveloppe', GEO_OBJET.STEnvelope().STAsText() AS Geo_Objet
FROM SIG.T_GEOMETRY;
Cet exemple dessine les lettres A et B
Exemple 15 Рidem pr̩c̩dent avec avec PostGreSQL / PostGis
CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('A', ST_GeomFromText('LINESTRING (0 0, 15 70, 25 70, 40 0,
31.42857 40, 8.57428 40 )', 0));
INSERT INTO SIG.T_GEOMETRY
VALUES ('B', ST_GeomFromText('LINESTRING (50 40, 50 0, 70 0, 82 5, 90 15, 90 25, 82 35,
70 40, 50 40, 50 70, 70 70, 80 65, 83 55, 80 45,
70 40)', 0));
SELECT 'Lettre : ' || GEO_NOM AS NOM, ST_AsText(GEO_OBJET) AS Geo_Objet
FROM SIG.T_GEOMETRY
UNION ALL
SELECT GEO_NOM || ' - enveloppe', ST_AsText(ST_Envelope(GEO_OBJET)) AS Geo_Objet
FROM SIG.T_GEOMETRY;
geo_nom geo_objet
--------------- ------------------------------------------------------------------
Lettre : A LINESTRING(0 0,15 70,25 70,40 0,31.42857 40,8.57428 40)
Lettre : B LINESTRING(50 40,50 0,70 0,82 5,90 15,90 25,82 35,70 40,50 40,
50 70,70 70,80 65,83 55,80 45,70 40)
A - enveloppe POLYGON((0 0,0 70,40 70,40 0,0 0))
B - enveloppe POLYGON((50 0,50 70,90 70,90 0,50 0))
Exemples 16 – avec MS SQL Server
CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('B', geometry::STGeomFromText('POLYGON ((50 0, 70 0, 82 5, 90 15, 90 25, 82 35,
70 40, 80 45, 83 55, 80 65, 70 70, 50 70,
50 40, 50 0))', 0));
SELECT GEO_NOM, GEO_OBJET.STAsText() AS OBJET
FROM SIG.T_GEOMETRY
UNION ALL
SELECT GEO_NOM + ' (enveloppe)', GEO_OBJET.STBoundary().STAsText()
FROM SIG.T_GEOMETRY;
Dans cet exemple l’objet bornant du polygone est une ligne brisée.
Exemple 17 - idem précédent avec avec PostGreSQL / PostGisCREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('B', ST_GeomFromText('POLYGON ((50 0, 70 0, 82 5, 90 15, 90 25, 82 35, 70 40,
80 45, 83 55, 80 65, 70 70, 50 70, 50 40, 50 0))',
0));
SELECT GEO_NOM, ST_AsText(GEO_OBJET) AS OBJET
FROM SIG.T_GEOMETRY
UNION ALL
SELECT GEO_NOM || ' (enveloppe)', ST_AsText(ST_Boundary(GEO_OBJET))
FROM SIG.T_GEOMETRY;
geo_nom objet
---------------- ----------------------------------------------------------------
B POLYGON ((50 0, 70 0, 82 5, 90 15, 90 25, 82 35, 70 40, 80 45,
83 55, 80 65, 70 70, 50 70, 50 40, 50 0))
B (enveloppe) LINESTRING (50 0, 70 0, 82 5, 90 15, 90 25, 82 35, 70 40,
80 45, 83 55, 80 65, 70 70, 50 70, 50 40, 50 0)
6.4 РM̩thodes testant les relations topologiques entre les objets
Les méthodes suivantes testent les relations topologiques entre deux objets. Elles renvoient
un Integer qui vaut 0 (Faux) ou 1 (Vrai).
Figures 4 – Relations topologiques
a) disjoint, b) touche,
c) chevauche, d) égale.
e) intersecte, f) contient.
Méthode |Description
-------------------------------------- |----------------------------------------------------
Disjoint (autre : Geometry): Integer |Retourne 1 (vrai) si l’objet géométrique est
|disjoint de l’autre objet géométrique.
-------------------------------------- |----------------------------------------------------
Touches (autre : Geometry) : Integer |Retourne 1 (vrai) si l’objet géométrique touche
|l’autre objet géométrique.
-------------------------------------- |----------------------------------------------------
Overlaps (autre : Geometry) : Integer |Retourne 1 (vrai) si l’objet géométrique chevauche
|l’autre objet géométrique.
-------------------------------------- |----------------------------------------------------
Equals (autre : Geometry) : Integer |Retourne 1 (vrai) si l’objet géométrique est
|strictement égal à l’autre objet géométrique.
-------------------------------------- |----------------------------------------------------
Intersects (autre : Geometry) : Integer|Retourne 1 (vrai) si l’objet géométrique possède une
|intersection spatiale avec l’autre objet géométrique
-------------------------------------- |----------------------------------------------------
Contains (autre : Geometry) : Integer |Retourne 1 (vrai) si l’objet géométrique contient
|spatialement l’autre objet géométrique.
--------------------------------------------------------------------------------------------
Exemple 18 – avec MS SQL Server
CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('POLY_________REF', 'POLYGON((0 0, 0 10, 4 10, 4 0, 0 0))');
INSERT INTO SIG.T_GEOMETRY
VALUES ('Polygon_00', 'POLYGON((0 7, 2 9, 4 7, 2 5, 0 7))'),
('Polygon_01', 'POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))'),
('Polygon_02', 'POLYGON((2 3, 2 5, 4 5, 4 3, 2 3))'),
('Polygon_03', 'POLYGON((3 5, 3 7, 5 7, 5 5, 3 5))'),
('Polygon_04', 'POLYGON((4 7, 4 9, 6 9, 6 7, 4 7))'),
('Polygon_05', 'POLYGON((5 9, 5 11, 7 11, 7 9, 5 9))'),
('Poly_99', 'POLYGON((0 10, 4 10, 4 0, 0 0, 0 10))');
SELECT T1.GEO_NOM AS Reference, T2.GEO_NOM AS Autre,
T1.GEO_OBJET.STDisjoint(T2.GEO_OBJET) AS Disjoint,
T1.GEO_OBJET.STTouches(T2.GEO_OBJET) AS Touche,
T1.GEO_OBJET.STOverlaps(T2.GEO_OBJET) AS Chevauche,
T1.GEO_OBJET.STEquals(T2.GEO_OBJET) AS Egale,
T1.GEO_OBJET.STIntersects(T2.GEO_OBJET) AS Intersecte,
T1.GEO_OBJET.STContains(T2.GEO_OBJET) AS Contient
FROM SIG.T_GEOMETRY AS T1
CROSS JOIN SIG.T_GEOMETRY AS T2
WHERE T1.GEO_NOM LIKE '%REF'
AND T2.GEO_NOM NOT LIKE '%REF'
Reference Autre Disjoint Touche Chevauche Egale Intersecte Contient
------------------ ------------ -------- ------ --------- ----- ---------- --------
POLY_________REF Polygon_00 0 0 0 0 1 1
POLY_________REF Polygon_01 0 0 0 0 1 1
POLY_________REF Polygon_02 0 0 0 0 1 1
POLY_________REF Polygon_03 0 0 1 0 1 0
POLY_________REF Polygon_04 0 1 0 0 1 0
POLY_________REF Polygon_05 1 0 0 0 0 0
POLY_________REF Poly_99 0 0 0 1 1 1
Exemple 19 Рidem pr̩c̩dent avec avec PostGreSQL / PostGis
CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);
INSERT INTO SIG.T_GEOMETRY
VALUES ('POLY_________REF', 'POLYGON((0 0, 0 10, 4 10, 4 0, 0 0))');
INSERT INTO SIG.T_GEOMETRY
VALUES ('Polygon_00', 'POLYGON((0 7, 2 9, 4 7, 2 5, 0 7))'),
('Polygon_01', 'POLYGON((1 1, 3 1, 3 3, 1 3, 1 1))'),
('Polygon_02', 'POLYGON((2 3, 2 5, 4 5, 4 3, 2 3))'),
('Polygon_03', 'POLYGON((3 5, 3 7, 5 7, 5 5, 3 5))'),
('Polygon_04', 'POLYGON((4 7, 4 9, 6 9, 6 7, 4 7))'),
('Polygon_05', 'POLYGON((5 9, 5 11, 7 11, 7 9, 5 9))'),
('Poly_99', 'POLYGON((0 10, 4 10, 4 0, 0 0, 0 10))');
SELECT T1.GEO_NOM AS Reference, T2.GEO_NOM AS Autre,
ST_Disjoint(T1.GEO_OBJET, T2.GEO_OBJET) AS Disjoint,
ST_Touches(T1.GEO_OBJET, T2.GEO_OBJET) AS Touche,
ST_Overlaps(T1.GEO_OBJET, T2.GEO_OBJET) AS Chevauche,
ST_Equals(T1.GEO_OBJET, T2.GEO_OBJET) AS Egale,
ST_Intersects(T1.GEO_OBJET, T2.GEO_OBJET) AS Intersecte,
ST_Contains(T1.GEO_OBJET, T2.GEO_OBJET) AS Contient
FROM SIG.T_GEOMETRY AS T1
CROSS JOIN SIG.T_GEOMETRY AS T2
WHERE T1.GEO_NOM LIKE '%REF'
AND T2.GEO_NOM NOT LIKE '%REF';
reference autre disjoint touche chevauche egale intersecte contient
------------------ ------------ -------- ------ --------- ----- ---------- --------
POLY_________REF Polygon_00 f f f f t t
POLY_________REF Polygon_01 f f f f t t
POLY_________REF Polygon_02 f f f f t t
POLY_________REF Polygon_03 f f t f t f
POLY_________REF Polygon_04 f t f f t f
POLY_________REF Polygon_05 t f f f f f
POLY_________REF Poly_99 f f f t t t
NOTA – Remarquez les subtiles différences : outre la dénomination des méthodes et leur syntaxe, PostGreSQL/PostGis renvoie une véritable valeur booléenne affichée sous forme t (true) et f (false) dans l’IHM PGadmin car rendant un type booléen, mais ceci n’est pas conforme au standard OGC qui spécifie que les méthodes doivent renvoyer un entier ayant pour valeur 0 ou 1.
6.5 – Méthodes DE-9IM et autour de…
Crosses (autre : Geometry) : Integer
Retourne 1 (vrai) si l’objet géométrique croise l’autre objet géométrique.
Il y a croisement si les deux conditions suivantes sont simultanément vraies :
- l’intersection des deux objets génère un objet géométrique de dimension inférieure à la dimension maximale des deux objets sources ;
- l’intersection est intérieure aux deux objets sources.
Within (autre : Geometry) : Integer
Retourne 1 (vrai) si l’objet géométrique est entièrement à l’intérieur de l’autre objet géométrique.
Relate (autre : Geometry, intersectionPatternMatrix : String) : Integer
Retourne 1 (vrai) si l’objet géométrique est lié à l’autre objet géométrique dans le cadre d’un motif de matrice intersectionnelle tel que défini par le modèle DE-9IM.
DE-9IM (Dimensionally Extended 9 Intersection Model) est une matrice présentant les neuf cas d’intersection entre deux objets et permet de tester globalement des dépendances topologiques. La matrice DE-9IM est représentée comme suit :
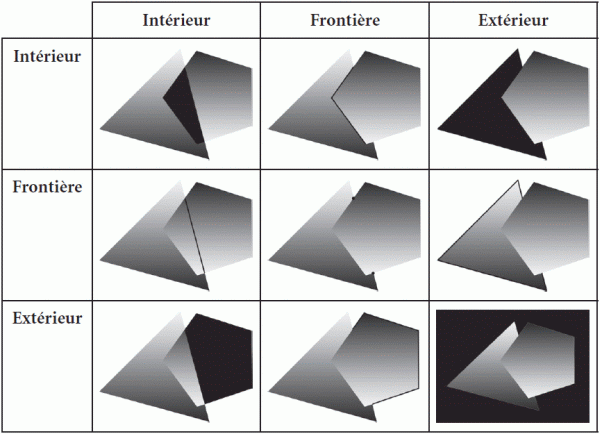
Figure 5 : Matrice d’intersection de deux régions spatiales (A triangle et B pentagone) suivant le modèle DE-9IM.
Dans les neuf images de la figure 5, on représente en noir l’objet géométrique résultant de la combinaison des propriétés Intérieur, Frontière et Extérieur entre les deux objets.
Nous avons ici représenté des polygones, mais ces propriétés s’appliquent à tout type d’objet spatial. Pour mieux en comprendre l’usage, voici une définition des termes utilisés :
• Frontière (Boundary) : la frontière d’un objet géométrique est un objet géométrique de dimension n –1 qui « encadre » l’objet. Par exemple, pour un polygone, la frontière est la ligne brisée qui en est le périmètre. Pour une ligne brisée, la frontière est constituée des deux points d’extrémité. Pour un point, la frontière est l’ensemble vide, comme c’est le cas d’une ligne brisée refermée sur elle-même (périmètre).
• Intérieur (Interior) : l’intérieur d’un objet géométrique est constitué par l’ensemble des points qui restent lorsque la frontière en est supprimée. Pour un point, l’intérieur est le point lui-même. Pour une ligne brisée, l’intérieur est la ligne brisée qui reste lorsqu’on a retiré les points d’extrémité. Pour un polygone, l’intérieur est la surface interne du polygone (moins les points du périmètre).
• Extérieur (Exterior) : l’extérieur d’un objet géométrique est « l’univers », une surface théorique qui enveloppe l’objet géométrique. On peut aussi dire que l’extérieur est tout sauf la frontière et l’intérieur.
On peut constater par exemple dans la figure 5 que l’intersection des frontières de deux polygones est un ensemble de points, donc un objet de dimension 0. Si l’on s’intéresse aux dimensions des objets représentant la matrice intersectionnelle de l’exemple 25, on obtient le tableau suivant :
--------------------------------------------------
| | Intérieur | Frontière | Extérieur |
|-------------------------------------------------
| Intérieur | 2 | 1 | 2 |
|-------------------------------------------------
| Frontière | 1 | 0 | 1 |
|-------------------------------------------------
| Extérieur | 2 | 1 | 2 |
--------------------------------------------------
La méthode Relate, permet d’interroger cette matrice avec une chaîne de neufs caractères représentant un motif d’interrogation pour les neuf cellules du tableau. Les caractères interprétés sont les suivants :
1 - un objet géométrique de dimension 1
2 - un objet géométrique de dimension 2
* - n’importe quelle valeur (joker)
T - (true) un objet géométrique de dimension ≥ 0 (l’objet existe)
F - (false) l’ensemble vide (l’objet n’existe pas)
Ainsi, le motif « 212101212 » représente exactement la matrice de l’exemple 25 et l’application de la fonction Relate, comme ci dessous donnerait 1 :
Exemple 20 – application de la fonction Relate
A.Relate(B, '212101212')
Mais on peut aussi utiliser les jokers T, F et *, et à nouveau, l’application de la fonction
dans l’exemple suivant donnerait 1 :
Exemple 21 – application de la fonction Relate avec des jokers dans le motif
A.Relate(B, 'TTT1*1TTT')
Suite en partie 2
--------
Frédéric Brouard, SQLpro - ARCHITECTE DE DONNÉES, http://sqlpro.developpez.com/
Expert bases de données relationnelles et langage SQL. MVP Microsoft SQL Server
www.sqlspot.com : modélisation, conseil, audit, optimisation, tuning, formation
* * * * * Enseignant CNAM PACA - ISEN Toulon - CESI Aix en Provence * * * * *
Quelle est la capacité de stockage des types GEOMETRY et GEOGRAPHY ?
Merci d’avance