La loi de Benford est une loi de distribution statistique permettant de vĂ©rifier qu’un ensemble de donnĂ©es numĂ©riques se comporte de manière naturelle. La plupart du temps, une dĂ©viation Ă cette loi peut indiquer que les donnĂ©es sont fausses ou truquĂ©es. Elle est en particulier appliquĂ©e par le fisc amĂ©ricain depuis les annĂ©es 80 et rĂ©cemment par le service des impĂ´ts en France pour dĂ©busquer les comptabilitĂ©s frauduleuses !
Cet article entend montrĂ© ce qu’est la Loi de Benford Ă l’aide d’un exemple de procĂ©dure stockĂ©e permettant d’analyser n’importe quelle colonne d’une table de votre base.
Un peu d’histoire
En 1881 l’astronome Simon Newcomb fait une communication dans l’American Journal of Mathematics pour signaler que dans beaucoup de collections de donnĂ©es numĂ©rique, la frĂ©quence d’apparition du premier chiffre significatif n suit une loi mathĂ©matique probabiliste de LOG10(1 + /n). Quelques annĂ©es auparavant, il a constatĂ© que les premières pages d’une table de logarithme sont plus usĂ©es que les dernières. Il s’intrigue de ce fait et se demande ce qui pousse les utilisateurs Ă consulter plus souvent les chiffres commençant par 1 que ceux commençant par un 9. HĂ©las, sa communication reste lettre morte. La formule ne convainc pas d’autant qu’aucune dĂ©monstration ne vient l’Ă©tayer.
Cinquante sept ans plus tard, la même distribution est redécouverte par Frank Benford qui rapporte ses observations effectuées sur 20 229 données de différente origines.
Cette loi prĂ©voit, que le premier chiffre significatif d’un nombre d’une sĂ©rie statistique quelconque ne suit pas une loi d’uniformitĂ© (Ă©quiprobabilitĂ© d’apparition d’un des chiffres entre 0 et 9), mais au contraire, que le chiffre 1 est largement prĂ©pondĂ©rant, le 2 un peu moins et ainsi de suite jusqu’au chiffre 9 qui est Ă l’inverse le moins frĂ©quent.
Loi Benford (aussi appelée Loi de Newcomb-Benford)
Chiffre Fréquence %
-------- ----------
1 30.10
2 17.61
3 12.49
4 9.69
5 7.92
6 6.69
7 5.80
8 5.12
9 4.58
Aussi paradoxale soit-elle cette loi est vĂ©rifiĂ©e pleinement dans certains domaines, approximativement dans d’autre et nullement dans un bon nombre. Aussi de nombreuses recherches tendent Ă rĂ©pondre aux questions suivantes :
- Quelles conditions générales doivent vérifier un ensemble de données numérique pour suivre la loi de Benford ?
- Pourquoi la plupart des données empiriques (constantes physiques, données économiques ou démographiques) vérifient-elles approximativement cette loi ?
C’est pourquoi une sĂ©rieuse mise en garde doit ici ĂŞtre apportĂ©e, et notamment de vĂ©rifier si elle s’applique bien au domaine que vous voulez scruter. A ce sujet, l’Ă©tude de Nicolas Gauvrit et Jean-Paul Delahaye constitue une bonne introduction (Pourquoi la Loi de Benford n’est pas Mystèrieuse).
En 1996 le mathĂ©maticien Terence HILL dĂ©montra la loi de Benford, mais en partant du principe que tous les nombres incriminĂ©s sont exprimĂ©s dans une certaine unitĂ© de mesure. Cette loi n’est donc pas universelle !
La loi de benford d’ordre 2…
Existe t-il une frĂ©quence d’apparition aussi particulière pour le second chiffre significatif d’un ensemble de nombre ? La rĂ©ponse est oui !
Le calcul de cette frĂ©quence s’Ă©tablit comme suit :
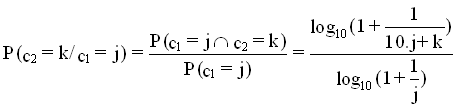
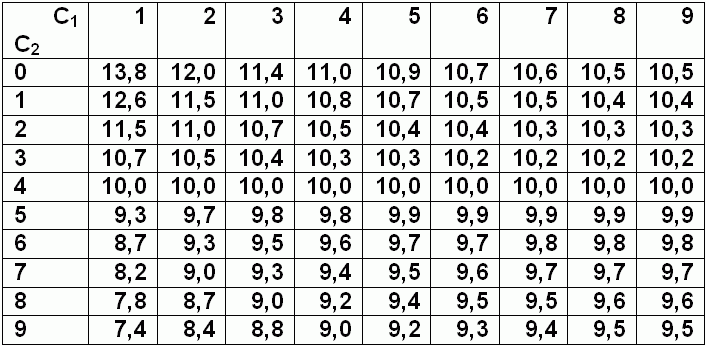
C1 étant le premier nombre et C2 le suivant. Les calculs de cette formule sont résumés dans le tableau suivant :
Comment prouver l’Ă©cart ?
Les statistiques nous offrent diffĂ©rents outils afin de savoir si l’ensemble des donnĂ©es confrontĂ©es Ă la loi de Benford s’en Ă©carte peu ou prou. Un des tests les plus simple est celui dit du khi-deux (Ă prononcer « qui carrĂ© »).
La formulation de ce test est la suivante :
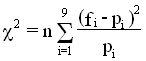
Pour la loi de Benford nous devons prendre le test du khi-deux avec 8 degrés de liberté (puisque neuf valeurs). Les seuils de rejets sont alors les suivants :
risque d'erreur (%) 90 50 30 20 10 5 1 0.1
seuil 3,49 7,34 9,52 11,03 13.36 15.51 20.09 26.12
Une procédure pour ce faire
Voici une procĂ©dure Ă©crite en Transact SQL, mais facile Ă adapter dans le langage procĂ©dural de votre SGBDR favori…
CREATE PROCEDURE dbo.P_BENFORD_TEST
@SCHEMA SYSNAME = 'dbo',
@TABLE SYSNAME,
@COLUMN SYSNAME,
@ECHANTILLON FLOAT = NULL -- en pourcentage
AS
SET NOCOUNT ON;
-- vérifications
IF NOT EXISTS(SELECT *
FROM INFORMATION_SCHEMA.COLUMNS
WHERE TABLE_SCHEMA = @SCHEMA
AND TABLE_NAME = @TABLE
AND COLUMN_NAME = @COLUMN)
BEGIN
RAISERROR(N'Aucune colonne de la table %s.%s ne porte le nom "%s".', 16, 1, @SCHEMA, @TABLE, @COLUMN);
RETURN;
END
IF NOT @ECHANTILLON > 0 AND @ECHANTILLON <= 100
BEGIN
RAISERROR(N'La valeur de l''échantillon doit être compris entre zéro et cent', 16, 1);
RETURN;
END
IF @ECHANTILLON = 100
SET @ECHANTILLON = NULL;
DECLARE @GUID UNIQUEIDENTIFIER, @SQL NVARCHAR(max), @TTNAME SYSNAME, @ECH NVARCHAR(64);
SET @ECH = COALESCE(' TABLESAMPLE ' + CAST(@ECHANTILLON AS VARCHAR(3)) +' PERCENT', '')
SET @GUID = NEWID();
SET @TTNAME = REPLACE(CAST(@GUID AS NVARCHAR(38)), '-', '');
-- création de la table pour stockage du résultat
SET @SQL = N'CREATE TABLE ##T_' + @TTNAME + '_BNF '
+ '(BNF_CHIFFRE SMALLINT, '
+ ' BNF_LOI_PC DECIMAL(4,2), '
+ ' BNF_LOI_NB BIGINT, '
+ ' BNF_STAT_PC DECIMAL(32,2),'
+ ' BNF_STAT_NB BIGINT, '
+ ' BNF_ECART_PC DECIMAL(4,2),'
+ ' BNF_ECART_ABS BIGINT,'
+ ' BNF_CHI_DEUX FLOAT);';
EXEC (@SQL);
-- alimentation des données de la table
SET @SQL = N'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC)'
+ ' VALUES (1, 100 * LOG10(1.0 + 1.0/1.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (2, 100 * LOG10(1.0 + 1.0/2.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (3, 100 * LOG10(1.0 + 1.0/3.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (4, 100 * LOG10(1.0 + 1.0/4.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (5, 100 * LOG10(1.0 + 1.0/5.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (6, 100 * LOG10(1.0 + 1.0/6.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (7, 100 * LOG10(1.0 + 1.0/7.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (8, 100 * LOG10(1.0 + 1.0/8.0));'
+ 'INSERT INTO ##T_' + @TTNAME + '_BNF (BNF_CHIFFRE, BNF_LOI_PC) '
+ ' VALUES (9, 100 * LOG10(1.0 + 1.0/9.0));';
EXEC (@SQL);
-- comptage
SET @SQL = N'WITH T AS (SELECT SUBSTRING(CAST([' + @COLUMN
+ '] AS VARCHAR(128)), 1, 1) AS N '
+ 'FROM [' + @SCHEMA +'].[' + @TABLE +'] '+ @ECH +' ), TT AS ( '
+ 'SELECT 1 AS N, SUM(CASE N WHEN 1 THEN 1 ELSE 0 END) AS C '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 2, SUM(CASE N WHEN 2 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 3, SUM(CASE N WHEN 3 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 4, SUM(CASE N WHEN 4 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 5, SUM(CASE N WHEN 5 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 6, SUM(CASE N WHEN 6 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 7, SUM(CASE N WHEN 7 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 8, SUM(CASE N WHEN 8 THEN 1 ELSE 0 END) '
+ 'FROM T '
+ 'UNION ALL '
+ 'SELECT 9, SUM(CASE N WHEN 9 THEN 1 ELSE 0 END) '
+ 'FROM T) '
+ 'UPDATE ##T_' + @TTNAME + '_BNF '
+ 'SET BNF_STAT_NB = C '
+ 'FROM ##T_' + @TTNAME + '_BNF AS S '
+ 'INNER JOIN TT '
+ ' ON S.BNF_CHIFFRE = TT.N';
EXEC (@SQL);
-- calcul relatifs
SET @SQL = N'UPDATE ##T_' + @TTNAME + '_BNF '
+ 'SET BNF_STAT_PC = 100.0 * BNF_STAT_NB / CAST( (SELECT SUM(BNF_STAT_NB) '
+ 'FROM ##T_' + @TTNAME + '_BNF ) AS FLOAT)';
EXEC (@SQL);
SET @SQL = N'UPDATE ##T_' + @TTNAME + '_BNF '
+ 'SET BNF_LOI_NB = BNF_LOI_PC * (SELECT SUM(BNF_STAT_NB) '
+ 'FROM ##T_' + @TTNAME + '_BNF ) / 100';
EXEC (@SQL);
SET @SQL = N'UPDATE ##T_' + @TTNAME + '_BNF '
+ 'SET BNF_ECART_PC = ABS(100 - ((BNF_STAT_PC / BNF_LOI_PC) * 100)), '
+ ' BNF_ECART_ABS = ABS(BNF_STAT_NB - BNF_LOI_NB)';
EXEC (@SQL);
SET @SQL = N'UPDATE ##T_' + @TTNAME + '_BNF '
+ 'SET BNF_CHI_DEUX = SQRT(CAST(SQUARE(BNF_ECART_ABS) AS FLOAT) '
+ '/ CAST(BNF_LOI_NB AS FLOAT))';
EXEC (@SQL);
-- affichage final
SET @SQL = N'SELECT BNF_CHIFFRE, BNF_LOI_PC, BNF_LOI_NB, BNF_STAT_PC, BNF_STAT_NB, '
+ ' CAST(BNF_ECART_PC AS DECIMAL(5,2)) AS BNF_ECART_PC, BNF_ECART_ABS, '
+ ' CAST(BNF_CHI_DEUX AS DECIMAL(32,2)) AS BNF_CHI_DEUX '
+ 'FROM (SELECT 0 AS O, * FROM ##T_' + @TTNAME + '_BNF '
+ ' UNION ALL '
+ ' SELECT 1, NULL, 100, SUM(BNF_LOI_NB), 100, SUM(BNF_STAT_NB), '
+ ' AVG(BNF_ECART_PC), AVG(BNF_ECART_ABS), SUM(BNF_CHI_DEUX) '
+ ' FROM ##T_' + @TTNAME + '_BNF) AS T '
+ 'ORDER BY O, BNF_CHIFFRE';
EXEC (@SQL);
SET @SQL = N'DROP TABLE ##T_' + @TTNAME + '_BNF ';
EXEC (@SQL);
GO
Exemple d’application :
EXEC dbo.P_BENFORD_TEST 'Sales', 'SalesOrderHeader', 'TotalDue' , NULL
RĂ©sultat obtenu :
BNF_CHIFFRE BNF_LOI_PC BNF_LOI_NB BNF_STAT_PC BNF_STAT_NB BNF_ECART_PC BNF_ECART_ABS BNF_CHI_DEUX
----------- ---------------- ----------------- --------------- ----------------- ---------------- ----------------- --------------
1 30.10 9470 17.80 5602 40.86 3868 39.75
2 17.61 5540 26.69 8397 51.56 2857 38.38
3 12.49 3929 13.93 4382 11.53 453 7.23
4 9.69 3048 7.69 2419 20.64 629 11.39
5 7.92 2492 6.44 2027 18.69 465 9.31
6 6.69 2105 8.72 2745 30.34 640 13.95
7 5.80 1824 6.56 2065 13.10 241 5.64
8 5.12 1611 8.53 2684 66.60 1073 26.73
9 4.58 1441 3.64 1144 20.52 297 7.82
NULL 100.00 31460 100.00 31465 30.43 1169 160.22
La dernière ligne montre les valeurs cumulĂ©es (BNF_LOI_PC, BNF_LOI_NB, BNF_STAT_PC, BNF_STAT_NB, BNF_CHI_DEUX) et moyenne (BNF_ECART_PC, BNF_ECART_ABS). On peut voir que ces donnĂ©es s’Ă©carte très profondĂ©ment de la loi de Benford !
Bibliographie :
Newcomb s., “Note on the frequency of use of the different digits in natural numbers”, American Journal of Mathematics 4, 1881, p. 39-40.
Benford f., “The law of anomalous numbers”, Proceedings of the American Philosophical Society 78, 1938, p. 127-131.
Hill T., “Base-invariance implies Benford’s law”, Proceedings of the American Mathematical Society 123, 1995(a), p. 887-895.
Hill T., “A statistical derivation of the Significant-Digit Law”, Statistical Science 10(4), 1995(b), p. 354-363.
Hill T., The first digit phenomenon, American Scientist 86 (July-August 1998), p. 358.
Gauvrit N, Delahaye J.-P. “Pourquoi la Loi de Benford n’est pas Mystèrieuse”, Math. & Sci. hum. / Mathematics and Social Sciences (46e annĂ©e, n° 182, 2008(2), p. 7–15) http://www.ehess.fr/revue-msh/pdf/N182R1280.pdf
Delahaye J.-P. , L’Ă©tonnante loi de Benford, Pour la Science, janvier 2007, p90-95
Webographie :
Tests du khi-deux :
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./c/chideuxtest.html
http://www.bibmath.net/formulaire/tablechideux.php3
http://www.aly-abbara.com/utilitaires/statistiques/khi_carre.html
http://fr.wikipedia.org/wiki/Test_du_%CF%87%C2%B2
—
Frédéric BROUARD, Spécialiste modélisation, bases de données, optimisation, langage SQL.
Le site sur le langage SQL et les S.G.B.D. relationnels : http://sqlpro.developpez.com/
Expert SQL Server http://www.sqlspot.com : audit, optimisation, tuning, formation
* * * * * Enseignant au CNAM PACA et Ă l’ISEN Ă Toulon * * * * *
