Ceci est la seconde partie de cet article sur les SIG avec SQL dans les SGBDR. La première partie est lisible ici : http://blog.developpez.com/sqlpro/p9414/langage-sql-norme/sql-et-systeme-d-information-geographiqu/

6.6 РM̩thodes de calcul

Ces méthodes rendent un résultat numérique ou géométrique calculé dont la précision n’est pas absolue : limitation du fait du nombre de chiffres significatif accepté, méthode d’interpolation utilisée…

Distance (autre : Geometry) : Double

Retourne la plus courte distance entre n’importe quel point des objets considérés.

Buffer (distance : Double) : Geometry

Retourne un objet géométrique dont les points sont ceux de l’objet initial augmenté de tous les points situés entre les points de l’objet initial et le périmètre de l’objet augmenté de la valeur distance.

ConvexHull () : Geometry

Retourne un objet géométrique qui encadre de manière convexe l’objet considéré.

Intersection (autre : Geometry) : Geometry

Retourne un objet géométrique qui représente l’ensemble des points d’intersection entre les deux instances géométriques.

Exemple 22 Рillustration de la m̩thode Distance avec MS SQL Server 2008

-- création d'une table des départements français 

CREATE TABLE SIG.T_DEPARTEMENT_DPT 

(DPT_ID                 INT NOT NULL IDENTITY(1, 1) PRIMARY KEY, 

 DPT_NOM                VARCHAR(50) NOT NULL UNIQUE, 

 DPT_GEO_MULTIPOLYGON   GEOGRAPHY); 

 

-- alimentation de cette table 

INSERT INTO SIG.T_DEPARTEMENT_DPT VALUES 

('Ain', 'POLYGON ((5.06055951589488 45.811744306399461, …), 

('Aisne', 'POLYGON ((3.1083954675119969 49.114811432157509, …), 

('Allier', 'POLYGON ((2.5476775274335068 46.127346346175912, …), 

('Alpes-De-Haute-Provence', 'POLYGON ((6.8999655257629229 44.366043387793653, …), 

('Alpes-Maritimes', 'POLYGON ((6.9123164947739042 43.4494664094551, …), 

('Ardèche', 'POLYGON ((4.6310945602737377 44.345306299517588, …), 

('Ardennes', 'POLYGON ((5.3723334734393688 49.623970307721876, …), 

('Ariège', 'POLYGON ((2.1341254808659471 42.647358383705992, …), 

('Aube', 'POLYGON ((4.2578104254276923 47.953109400478681, …), 

('Aude', 'POLYGON ((3.2273034676371992 43.202217323178772, …), 

('Aveyron', 'POLYGON ((3.3659554513873218 44.172550271233618, …), 

('Bas-Rhin', 'POLYGON ((7.6411035794877478 49.059669305204849, …), 

('Bouches-Du-Rhône', 'POLYGON ((5.7380864179977493 43.732521301301617, …), 

('Calvados', 'POLYGON ((0.47600947531881843 49.002086309376423, …), 

('Cantal', 'POLYGON ((3.3602164963988059 44.979824306980234, …), 

('Charente', 'POLYGON ((0.61320049334679538 45.685100404765549, …), 

('Charente-Maritime', 'MULTIPOLYGON (((-1.236996412907297 45.758888317927088, …), 

… 

 

-- recherche des départements distants de moins de 5 km mais ne se touchant pas 

SELECT D1.DPT_NOM, D2.DPT_NOM,  

       D1.DPT_GEO_MULTIPOLYGON.STDistance(D2.DPT_GEO_MULTIPOLYGON) / 1000.0 AS DISTANCE_KM 

FROM   SIG.T_DEPARTEMENT_DPT AS D1 

       INNER JOIN SIG.T_DEPARTEMENT_DPT AS D2 

             ON D1.DPT_GEO_MULTIPOLYGON.STIntersects(D2.DPT_GEO_MULTIPOLYGON) = 0 

                AND D1.DPT_ID < D2.DPT_ID 

WHERE  D1.DPT_GEO_MULTIPOLYGON.STDistance(D2.DPT_GEO_MULTIPOLYGON) / 1000.0 <= 5 

ORDER  BY DISTANCE_KM DESC; 

 

DPT_NOM              DPT_NOM             DISTANCE_KM 

-------------------- ------------------- ---------------------- 

Drôme                Loire               4,94561313219237 

Moselle              Vosges              4,03579921242316 

Loire-Atlantique     Mayenne             2,97422727798512 

Calvados             Seine-Maritime      2,27080851352109

L’exemple ci-dessus montre une requête faisant une auto-jointure spatiale et recherche les départements qui ne sont pas voisins (intersection des frontières) et sont distants de moins de 5 km.

Exemple 23 РVoici la m̻me requ̻te avec PostGreSQL / PostGis :

SELECT D1.DPT_NOM, D2.DPT_NOM, 

       ST_Distance(D1.DPT_GEO_MULTIPOLYGON, D2.DPT_GEO_MULTIPOLYGON) / 1000.0 AS DISTANCE_KM 

FROM   SIG.T_DEPARTEMENT_DPT AS D1 

       INNER JOIN SIG.T_DEPARTEMENT_DPT AS D2 

             ON ST_Intersects(D1.DPT_GEO_MULTIPOLYGON, D2.DPT_GEO_MULTIPOLYGON) = 0 

                AND D1.DPT_ID < D2.DPT_ID 

WHERE  ST_Distance(D1.DPT_GEO_MULTIPOLYGON, D2.DPT_GEO_MULTIPOLYGON) / 1000.0 <= 5 

ORDER BY DISTANCE_KM DESC;

Exemple 24 Рillustration de la m̩thode Buffer avec MS SQL Server 2008

CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry); 

 

INSERT INTO SIG.T_GEOMETRY 

VALUES ('A', 'LINESTRING (0 0, 15 70, 25 70, 40 0, 31.42857 40, 8.57428 40 )'); 

 

SELECT GEO_NOM, 

       GEO_OBJET.STAsText() AS OBJET_TXT, 

       GEO_OBJET AS OBJET 

FROM   SIG.T_GEOMETRY 

UNION  ALL 

SELECT GEO_NOM + ' (buffer)', 

       GEO_OBJET.STBuffer(5).STAsText(), 

       GEO_OBJET.STBuffer(5) 

FROM   SIG.T_GEOMETRY; 

 

GEO_NOM     OBJET_TXT 

----------- ----------------------------------------------------------------------- 

A           LINESTRING (0 0, 15 70, 25 70, 40 0, 31.42857 40, 8.57428 40) 

A (buffer)  POLYGON ((-0.041054725646972656 -5.0008220672607422, 0.20717716217041016…

Exemple 25 Рillustration de la m̩thode ConvexHull avec MS SQL Server 2008

CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry);

INSERT INTO SIG.T_GEOMETRY
VALUES (‘B’, ‘POLYGON ((50 0, 70 0, 82 5, 90 15, 90 25, 82 35, 70 40,
80 45, 83 55, 80 65, 70 70, 50 70, 50 40, 50 0))’);

SELECT GEO_NOM,
GEO_OBJET.STAsText() AS OBJET_TXT
FROM SIG.T_GEOMETRY
UNION ALL
SELECT GEO_NOM + ‘ (enveloppe convexe)’,
GEO_OBJET.STConvexHull().STAsText()
FROM SIG.T_GEOMETRY;

GEO_NOM OBJET_TXT
——————— ——————————————————–
B POLYGON ((50 0, 70 0, 82 5, 90 15, 90 25, 82 35, 70 40,
80 45, 83 55, 80 65, 70 70, 50 70, 50 40, 50 0))
B (enveloppe convexe) POLYGON ((90 15, 90 25, 83 55, 80 65, 70 70, 50 70,
50 40, 50 0, 70 0, 82 5, 90 15))

Exemple 26 Рillustration de la m̩thode Intersection avec MS SQL Server 2008

CREATE TABLE T_GEO (GEO_NOM VARCHAR(16), GEO_OBJET GEOMETRY); 

 

-- insertion d’un carré 

INSERT INTO T_GEO (GEO_NOM, GEO_OBJET) 

VALUES (‘Un polygone’, 'POLYGON ((0 0, 0 1, 1 1, 1 0, 0 0))'); 

 

-- insertion d’une ligne oblique qui coupe en diagonale le carré 

INSERT INTO T_GEO (GEO_NOM, GEO_OBJET) 

VALUES (‘Une ligne’, 'LINESTRING(0 0, 1 1)'); 

 

-- intersection du carré et de la ligne, ainsi que du périmètre du carré avec la ligne 

SELECT T1.GEO_NOM AS GEO1, T1.GEO_OBJET.STAsText() AS OBJ1, 

       T2.GEO_NOM AS GEO2, T2.GEO_OBJET.STAsText() AS OBJ2, 

       T1.GEO_OBJET.STIntersection(T2.GEO_OBJET).STAsText() AS Inter, 

       T1.GEO_OBJET.STBoundary().STIntersection(T2.GEO_OBJET).STAsText() AS InterFrontiere 

FROM   T_GEO AS T1 

       CROSS JOIN T_GEO AS T2 

WHERE  T1.GEO_NOM LIKE '%polygone%' 

  AND  T2.GEO_NOM LIKE '%ligne%'; 

 

GEO1         OBJ1                GEO2       OBJ2        Inter       InterFrontiere 

------------ ------------------- ---------- ----------- ----------- -------------- 

Un polygone  POLYGON             Une ligne  LINESTRING  LINESTRING  MULTIPOINT ((0 0, 0 1, (0 0, 1 1) (1 1, 0 0) ((1 1), (0 0)) 1 1, 1 0, 0 0))

Exemple 27 РVoici la m̻me requ̻te avec PostGreSQL / PostGis :

SELECT T1.GEO_NOM AS GEO1, ST_AsText(T1.GEO_OBJET) AS OBJ1, 

       T2.GEO_NOM AS GEO2, ST_AsText(T2.GEO_OBJET) AS OBJ2, 

       ST_AsText(Intersection(T1.GEO_OBJET, T2.GEO_OBJET)) AS Inter, 

       ST_AsText(Intersection(Boundary(T1.GEO_OBJET), T2.GEO_OBJET)) AS InterFrontiere 

FROM   T_GEO AS T1 

       CROSS JOIN T_GEO AS T2 

WHERE  T1.GEO_NOM LIKE '%polygone%' 

  AND  T2.GEO_NOM LIKE '%ligne%';

Le résultat de l’intersection d’un polygone avec une ligne brisée est une ligne brisée. Si
l’on désire obtenir les points de contacts entre la ligne brisée et le périmètre du polygone,
il faut obtenir la frontière du polygone à l’aide de la méthode Boundary. Il en résulte un
objet de type multipoint.

6.7 РM̩thodes interg̩om̩triques

Union (autre : Geometry) Geometry

Retourne un objet géométrique qui est l’union des deux objets géométriques.

Difference (autre : Geometry) Geometry

Retourne un objet géométrique qui est la différence asymétrique entre les deux objets

SymDifference (autre : Geometry) Geometry

Retourne un objet géométrique qui est la différence symétrique entre les deux objets

NOTA :

A.SymDifference(B) = A.Difference(B).Union(A.Difference(A)) = B.SymDifference(A).

Exemple 28 Рillustration de la m̩thode Union avec MS SQL Server 2008 :

-- création d'une table des départements avec le nom de région 

CREATE TABLE SIG.T_DEPARTEMENT_REGION_DRG 

(DRG_ID                INT NOT NULL IDENTITY(1, 1) PRIMARY KEY, 

 DRG_NOM_DEPARTEMENT   VARCHAR(50) NOT NULL UNIQUE, 

 DRG_NOM_REGION        VARCHAR(50), 

 DRG_GEO_MULTIPOLYGON  GEOGRAPHY)   

 

-- alimentation de cette table 

INSERT INTO SIG.T_DEPARTEMENT_DPT VALUES  

('Ain', 'RHONE-ALPES', 'POLYGON ((5.06055951589488 45.811744306399461,   ...), 

('Aisne', 'PICARDIE', 'POLYGON ((3.1083954675119969 49.114811432157509,  ...), 

('Allier', 'AUVERGNE', 'POLYGON ((2.5476775274335068 46.127346346175912, ...), 

('Alpes-De-Haute-Provence', 'PROVENCE-ALPES-COTE-D'AZUR', 'POLYGON (6.89 ...), 

('Alpes-Maritimes', 'PROVENCE-ALPES-COTE-D'AZUR', 'POLYGON ((6.912316494 ...), 

('Ardèche', 'RHONE-ALPES', 'POLYGON ((4.6310945602737377 44.345306299517 ...), 

('Ardennes', 'CHAMPAGNE-ARDENNE', 'POLYGON ((5.3723334734393688 49.62397 ...), 

... 

 

-- calcul des objets géographique représentant les régions  

WITH 

T0 AS -- numérotation des départements par ordre de nom avec rupture par région 

(SELECT *, ROW_NUMBER()  

           OVER(PARTITION BY DRG_NOM_REGION ORDER BY DRG_NOM_DEPARTEMENT) AS N 

 FROM   SIG.T_DEPARTEMENT_REGION_DRG), 

T1 AS -- obtention du numéro le plus élevé pour chaque région 

(SELECT DRG_NOM_REGION, MAX(N) AS NMAX 

 FROM   T0 

  GROUP BY DRG_NOM_REGION),  

T2 AS -- Union récursive des objets géométriques d'une même région 

(SELECT DRG_NOM_REGION, N, DRG_GEO_MULTIPOLYGON 

 FROM   T0 

 WHERE  N = 1 

 UNION  ALL 

 SELECT T0.DRG_NOM_REGION, T0.N, 

        T0.DRG_GEO_MULTIPOLYGON.STUnion(T2.DRG_GEO_MULTIPOLYGON) 

 FROM   T0 

        INNER JOIN T2 

              ON T0.N = T2.N + 1 

                 AND T2.DRG_NOM_REGION = T0.DRG_NOM_REGION) 

-- requête finale 

SELECT * 

FROM   T1 

       INNER JOIN T2 

             ON T1.DRG_NOM_REGION = T2.DRG_NOM_REGION 

                AND N = NMAX; 

-- l'objet géométrique décrivant la région est celui qui a concaténé  

-- tous les départements (N = NMAX)

Cette requête utilise la technique des CTE (Common Table Expression – en français expression de table) afin de numéroter les départements dans l’ordre alphabétique puis de concaténer à l’aide de la méthode Union et par récursion les départements les uns aux autres tant qu’ils appartiennent à la même région.

Exemple 29 - illustration des méthodes Difference et SymDifference avec MS SQL Server 2008 :

CREATE TABLE T_GEO (GEO_NOM VARCHAR(24), GEO_OBJET GEOMETRY); 

 

INSERT INTO T_GEO  

   VALUES ('Rectangle grand', 'POLYGON ((1 1 , 1 5, 3 5, 3 1, 1 1))'); 

INSERT INTO T_GEO  

   VALUES ('Rectangle petit', 'POLYGON ((2 2, 4 2, 4 3, 2 3, 2 2))'); 

 

SELECT GEO_NOM, GEO_OBJET.STAsText()  AS GEO_OBJET 

FROM T_GEO; 

 

GEO_NOM          GEO_OBJET 

---------------- ------------------------------------- 

Rectangle grand  POLYGON ((1 1, 1 5, 3 5, 3 1, 1 1)) 

Rectangle petit  POLYGON ((2 2, 4 2, 4 3, 2 3, 2 2)) 

 

SELECT G1.GEO_OBJET.STDifference(G2.GEO_OBJET).STAsText() AS OBJET,  

       'Difference 1-2' AS Nom 

FROM   T_GEO AS G1 

       CROSS JOIN T_GEO AS G2 

WHERE  G1.GEO_NOM LIKE '%grand' 

  AND  G2.GEO_NOM LIKE '%petit' 

UNION  ALL 

SELECT G2.GEO_OBJET.STDifference(G1.GEO_OBJET).STAsText() AS OBJET,  

       'Difference 2-1'  AS Nom 

FROM   T_GEO AS G1 

       CROSS JOIN T_GEO AS G2 

WHERE  G1.GEO_NOM LIKE '%grand' 

  AND  G2.GEO_NOM LIKE '%petit'; 

 

Nom              OBJET 

---------------- --------------------------------------------------------- 

Difference 1-2   POLYGON ((1 1, 3 1, 3 2, 2 2, 2 3, 3 3, 3 5, 1 5, 1 1)) 

Difference 2-1   POLYGON ((3 2, 4 2, 4 3, 3 3, 3 2)) 

 

SELECT G1.GEO_OBJET.STSymDifference(G2.GEO_OBJET).STAsText()  AS OBJET,  

      'Differences' 

FROM   T_GEO AS G1 

       CROSS JOIN T_GEO AS G2 

WHERE  G1.GEO_NOM LIKE '%grand' 

  AND  G2.GEO_NOM LIKE '%petit'; 

 

Nom              OBJET 

-----------      --------------------------------------------------------------- 

Differences      MULTIPOLYGON (((3 2, 4 2, 4 3, 3 3, 3 2)),  

                               ((1 1, 3 1, 3 2, 2 2, 2 3, 3 3, 3 5, 1 5, 1 1)))

6.8 РM̩thodes sp̩cifiques

6.8.1 РM̩thodes applicables au type POINT :

X(), Y(), Z(), M() : ces méthodes retournent respectivement les coordonnées X, Y, Z (élévation) et M (mesure) d’un point.

6.8.2 РM̩thodes applicables aux types LINESTRING et MULTILINESTRING :

StartPoint() geometry

Premier point d’une ligne brisée

EndPoint() geometry

Dernier point d’une ligne brisée

IsRing() Integer

Renvoie 1 si la ligne brisée est refermée sur elle même (premier et dernier point sont identiques)

Length() float

Renvoie la longueur d’une ligne brisée

NumPoints() integer

Renvoi le nombre de point définissant une ligne brisée

SPointN(position : integer) geometry

Retourne le Neme point définissant une ligne brisée

Exemple 30 Рillustration des m̩thodes sp̩cifique au type LINESTRING avec PostGreSQL / PostGis :

CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry); 

 

INSERT INTO SIG.T_GEOMETRY 

   VALUES ('A', 'LINESTRING (0 0, 15 70, 25 70, 40 0, 31.42857 40, 8.57428 40  )'); 

INSERT INTO SIG.T_GEOMETRY 

   VALUES ('B', 'LINESTRING (50 40, 50  0, 70  0, 82  5, 90 15, 90 25,  

                        82 35, 70 40, 50 40, 50 70, 70 70, 80 65,  

                        83 55, 80 45, 70 40)'); 

                         

SELECT GEO_NOM,   

       ST_AsText(ST_StartPoint(GEO_OBJET)) AS Debut,   

       ST_AsText(ST_EndPoint(GEO_OBJET)) AS Fin, 

       ST_IsRing(GEO_OBJET) AS Clos, 

       ST_Length(GEO_OBJET) AS Longueur,      

       ST_NumPoints(GEO_OBJET) AS NBP, 

       ST_AsText(ST_PointN(GEO_OBJET, ST_NumPoints(GEO_OBJET)-1)) AS AvantDernierPoint 

FROM   SIG.T_GEOMETRY; 

      

GEO_NOM  Debut        Fin               Clos  Longueur  NBP AvantDernierPoint 

-------- ------------ ----------------- ----- --------- --- ------------------ 

A        POINT(0 0)   POINT(8.57428 40) f     216,9405  6   POINT(31.42857 40) 

B        POINT(50 40) POINT(70 40)      f     234,8537  15  POINT(80 45)

6.8.3 РM̩thodes applicables au type POLYGON :

ExteriorRing() geometry

Retourne une ligne brisée qui représente l’anneau extérieur d’un polygone (enveloppe)

InteriorRings()  geometry

Retourne un ensemble de lignes brisées qui représente les anneaux intérieur d’un polygone contenant des « trous »

NumInteriorRing()  integer

Retourne le nombre d’anneaux intérieurs

InteriorRingN(position integer) geometry

Retourne une ligne brisées qui représente l’anneau intérieur de rang N d’un polygone contenant des « trous », N étant compté de l’extérieur vers l’intérieur.

Exemple 31 - illustration des méthodes spécifique au type POLYGON avec PostGreSQL / PostGis :

CREATE TABLE SIG.T_GEOMETRY (GEO_NOM VARCHAR(24), GEO_OBJET geometry); 

 

-- insertion du polygone de la figure 30 dans la table  

INSERT INTO SIG.T_GEOMETRY 

VALUES ('POLY TROU',  

'POLYGON  

((0 -10, 0.51459884643554688 -9.9869880676269531, 1.0224418640136719..., 0 -10), 

 (0 -20, 1.0291976928710938 -19.973976135253906, 2.0448837280273438 ..., 0 -20), 

 (0 -30, 1.5437955856323242 -29.960964202880859, 3.0673255920410156 ..., 0 -30), 

 (0 -40, 2.0583953857421875 -39.947952270507812, 4.0897674560546875 ..., 0 -40))'); 

 

SELECT GEO_NOM, ST_AsText(ST_ExteriorRing(GEO_OBJET)) AS OBJ 

FROM   SIG.T_GEOMETRY 

UNION  ALL 

SELECT GEO_NOM, ST_AsText(ST_InteriorRingN(GEO_OBJET, 2)) 

FROM   SIG.T_GEOMETRY; 

 

geo_nom     obj 

----------- ------------------------------------------------------------------- 

POLY TROU   LINESTRING(0 -10,0.514598846435547 -9.98698806762695, ... 0 -10) 

POLY TROU   LINESTRING(0 -30,1.54379558563232 -29.9609642028809,  ... 0 -30)

La requête extrait la ligne brisée enveloppant le polygone ainsi que l’anneau intérieur de rang 2

6.8.4 РM̩thodes applicables aux types POLYGON et MULTIPOLYGON :

Area() float

Renvoie la superficie (dans l’unité de mesure spécifique par le SRID pour les instances géographiques)

Centroid() geometry

Retourne le centre géométrique

PointOnSurface() geometry

Retourne un point arbitraire situé à l’intérieur de l’instance

Exemple 32 Рutilisation de la m̩thode Area avec MS SQL Server 2008 :

WITH 

T0 AS 

(SELECT DPT_NOM, 

        RANK() OVER(ORDER BY DPT_GEO_MULTIPOLYGON.STArea() DESC) AS RANG, 

        DPT_GEO_MULTIPOLYGON.STArea() AS Superfi cie 

 FROM SIG.T_DEPARTEMENT_DPT) 

SELECT DPT_NOM, Superfi cie / 1000 AS KM_CARRE 

FROM   T0 

WHERE  RANG <= 10; 

 

DPT_NOM                 KM_CARRE 

----------------------- ------------ 

Gironde                 10043647,663 

Landes                   9255928,6953 

Dordogne                 9085558,6524 

Côte-d’Or                8922004,1729 

Aveyron                  8901788,0343 

Saône-et-Loire           8623363,2000 

Marne                    8468321,1468 

Puy-De-Dôme              7904916,2467 

Isère                    7850439,8607 

Pyrénées-Atlantiques     7469226,7966

La requête utilise la table des départements vus à l’exemple 28 pour retourner les 10 départements les plus grands dans l’ordre décroissant.

6.8.5 РM̩thodes applicables au type GEOMETRYCOLLECTION :

ST_NumGeometries() : integer

Retourne le nombre d’objet de la collection géométrique

ST_GeometryN (position INTEGER) : geometry

Retourne l’objet géométrique à la position N dans la collection

7 – Et quoi encore ?

Le présent article ne nous laisse pas de place pour tout traiter. Le livre SQL, collection synthex, 3e édition « SQL (3e édition) », collection Synthex – Pearson Education 2010 consacre un chapitre de près de 50 pages sur le sujet du SIG SQL.
Vous y trouverez donc en sus les éléments suivants :

• les jointures spatiales
• les contraintes spatiales
• les vues spatiales et diverses requêtes
• l’indexation spatiales

Le tout avec un exemple d’application de système de navigation par GPS.
Le chapitre se termine par une note sur la prospective en matière de SIG dans les SGBDR.

CONCLUSION : comparaison PostGreSQL / PostGIS vs SQL Server 2008

Il semble bien que les méthodes disponible dans l’un et l’autre système soient quasiment identiques. C’est vrai mais a un détail près : l’aptitude de postGreSQL / PostGIS a faire réellement du spatiale sur l’écorce terrestre. Et là la partie est plutôt largement gagnée par SQL Server. En effet quand on regarde de près les deux systèmes, la différence la plus criante entre MS SQL Server et PostGIS (PostGreSQL) porte sur l’utilisation des différents référentiels spatial. PostGreSQL n’est capable d’utiliser que le référentiel mondial (SRID 4326 : WGS 84) tandis que SQL Server en gère 390 dont le français (4171 – RGF 93) et ceux des différents territoires d’outremer (Voir ci après). Cela limite considérablement l’utilisation de PostGIS sur le plan national, car les Lois nationales imposent la plupart du temps et pour chaque état d’utiliser un SRID local. (voir annexe 1) Par exemple, en France métropolitaine, les mairies, le cadastre et les collectivités territoriale comme les ministères, doivent utiliser le SRID 4171. Il s’agit d’une obligation légale… Est-ce là une des raisons pour lesquelles l’IGN vient d’introduire SQL Server en complément de postGreSQL ?
De plus cette limitation rend inopérant certains méthodes comme Dimension, GeometryType et bien entendu Srid dans le type GEOGRAPHY. Il faut alors passer par un type GEOMETRY, c’est à dire sans la courbure terrestre.

Notons en sus quelques différences importantes :

• La fonction MakeValid() (voir annexe 2) de MS SQL Server (conforme à l’OGC) permet de recalculer un objet géométrique afin de le rendre opérable en tant que tel. Elle n’existe pas sous PostGreSQL et son absence est susceptible de provoquer dans les calculs des erreurs liées notamment aux opérateurs géométriques. En effet, on doit noter que la transformation résultante peut changer la nature des objets pour les rendre plus conforme a leur usage lorsqu’ils sont mal définis.
• PostGIS offre une fonction d’agrégation des objets géométrique afin de les « concaténer », de nom ST_Union. Pour faire cette même chose sous MS SQL Server il faut utiliser une requête récursive, ce qui est moins pratique.

ANNEXE 1 : Les SRID utilisable pour la France (MS SQL Server) :

SRID    Désignation 

------- ----------------------------------------------------------------- 

4171    RGF93 - Reseau Geodesique Francais 1993 

4275    NTF - Nouvelle Triangulation Francaise 

4624    RGFG95 - Reseau Geodesique Francais Guyane 1995 

4640    RRAF 1991 - Reseau de Reference des Antilles Francaises 1991 

4687    RGPF - Reseau Geodesique de la Polynesie Francaise 

4807    NTF (Paris) - Nouvelle Triangulation Francaise (Paris) 

4901    ATF (Paris) - Ancienne Triangulation Francaise (Paris) 

4965    RGF93 - Reseau Geodesique Francais 1993 

4967    RGFG95 - Reseau Geodesique Francais Guyane 1995 

4973    RRAF 1991 - Reseau de Reference des Antilles Francaises 1991 

4999    RGPF - Reseau Geodesique de la Polynesie Francaise

ANNEXE 2 : MakeValid et validation de forme géométriques

Voici un exemple de forme géométrique, au départ invalide, rendue valide par la fonction MakeValid de MS SQL Server :

Le polygone saisi est invalide, car le dessin des lignes périmériques se croisent. Or une telle forme de polygone n’existe pas à l’état naturel et rendrait faux certains calculs.

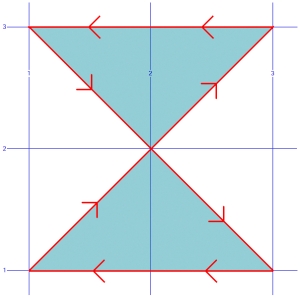
La méthode MakeValid transforme ce polygone en un multipolygone composé de deux triangles, comme ceci :

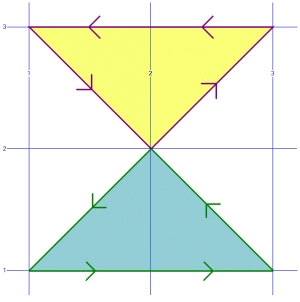
et le résultat est le suivant :
MULTIPOLYGON (((2 2, 3 3, 1 3, 2 2)), ((1 1, 3 1, 2 2, 1 1)))

-------- 

Frédéric Brouard, SQLpro - ARCHITECTE DE DONNÉES, http://sqlpro.developpez.com/ 

Expert bases de données relationnelles et langage SQL. MVP Microsoft SQL Server 

www.sqlspot.com : modélisation, conseil, audit, optimisation, tuning, formation 

* * * * *  Enseignant CNAM PACA - ISEN Toulon - CESI Aix en Provence  * * * * *